题目内容
如图,真空中有一匀强电场,方向沿Ox正方向,若质量为m、电荷量为q的带电微粒从O点以初速v沿Oy方向进入电场,经△t时间到达A点,此时速度大小也是vo,方向沿Ox轴正方向,如图所示.求:(1)从O点到A点的时间△t.
(2)该匀强电场的场强E及OA连线与Ox轴的夹角θ.
(3)若设O点电势为零,则A点电势多大.
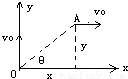
【答案】分析:(1)由题意,微粒到达A点时的速度大小与初速度大小相等,都是vo,说明微粒的重力不能忽略.微粒水平方向受到电场力,竖直方向受到重力作用,两个力都是恒力,运用运动的分解法:竖直方向微粒做竖直上抛运动,水平方向做初速度为零的匀加速运动.由速度公式研究竖直方向的运动情况即可求出时间△t.
(2)在x、y两个方向上微粒的分运动时间相等,由速度公式研究水平方向的加速度,由牛顿第二定律求出匀强电场的场强E.由位移公式x=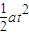 分别求出x和y,再求解OA连线与Ox轴的夹角θ.
分别求出x和y,再求解OA连线与Ox轴的夹角θ.
(3)根据动能定理求解OA间的电势差UOA,而UOA=φO-φA,φO=0,可求出φA.
解答:解:分析带电微粒的运动特征:微粒水平方向受到电场力,做初速度为零的匀加速运动;竖直方向受到重力作用,做匀减速运动.
(1)在竖直方向上,有 0-v=-g?△t,得△t=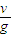 .
.
(2)在水平方向上,有 v=ax?△t=ax?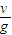 ,得ax=g
,得ax=g
由qE=max,得E=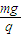
图中x=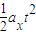 =
=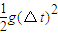 ,y=
,y=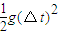
所以x=y.故OA连线与Ox轴的夹角θ=45°.
(3)从O到A,由动能定理得
-mgy+qUOA=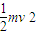 -
-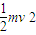
得 UOA=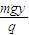 =
=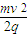
而UOA=φO-φA,φO=0,则φA=-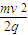
答:
(1)从O点到A点的时间△t为 .
.
(2)该匀强电场的场强E为 ,OA连线与Ox轴的夹角θ为45°.
,OA连线与Ox轴的夹角θ为45°.
(3)若设O点电势为零,则A点电势为- .
.
点评:本题是带电微粒在复合场中运动的问题,由于微粒所受的力是恒力,运用运动的分解法研究,根据动能定理求解电势差.
(2)在x、y两个方向上微粒的分运动时间相等,由速度公式研究水平方向的加速度,由牛顿第二定律求出匀强电场的场强E.由位移公式x=
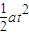 分别求出x和y,再求解OA连线与Ox轴的夹角θ.
分别求出x和y,再求解OA连线与Ox轴的夹角θ.(3)根据动能定理求解OA间的电势差UOA,而UOA=φO-φA,φO=0,可求出φA.
解答:解:分析带电微粒的运动特征:微粒水平方向受到电场力,做初速度为零的匀加速运动;竖直方向受到重力作用,做匀减速运动.
(1)在竖直方向上,有 0-v=-g?△t,得△t=
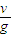 .
.(2)在水平方向上,有 v=ax?△t=ax?
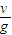 ,得ax=g
,得ax=g由qE=max,得E=
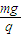
图中x=
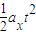 =
=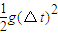 ,y=
,y=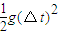
所以x=y.故OA连线与Ox轴的夹角θ=45°.
(3)从O到A,由动能定理得
-mgy+qUOA=
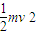 -
-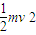
得 UOA=
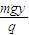 =
=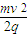
而UOA=φO-φA,φO=0,则φA=-
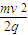
答:
(1)从O点到A点的时间△t为
 .
.(2)该匀强电场的场强E为
 ,OA连线与Ox轴的夹角θ为45°.
,OA连线与Ox轴的夹角θ为45°.(3)若设O点电势为零,则A点电势为-
 .
.点评:本题是带电微粒在复合场中运动的问题,由于微粒所受的力是恒力,运用运动的分解法研究,根据动能定理求解电势差.

练习册系列答案
相关题目
 如图,真空中有一匀强电场,方向沿Ox正方向,若质量为m、电荷量为q的带电微粒从O点以初速v0沿Oy方向进入电场,经△t时间到达A点,此时速度大小也是vo,方向沿Ox轴正方向,如图所示.求:
如图,真空中有一匀强电场,方向沿Ox正方向,若质量为m、电荷量为q的带电微粒从O点以初速v0沿Oy方向进入电场,经△t时间到达A点,此时速度大小也是vo,方向沿Ox轴正方向,如图所示.求:

