题目内容
匀强电场中有a、b、c三点.在以它们为顶点的三角形中, ∠a=30°、∠c=90°,.电场方向与三角形所在平面平行.已知a、b和c点的电势分别为 V、
V、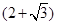 V和2 V.该三角形的外接圆上最低、最高电势分别为(
)
V和2 V.该三角形的外接圆上最低、最高电势分别为(
)

A. V、
V、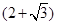 V B.0 V、4 V
V B.0 V、4 V
C.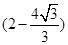 V、
V、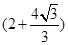 D.0 V、
D.0 V、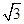 V
V
【答案】
B
【解析】在匀强电场中,任意一条直线上的电势降落时均匀的,所以ab两点的中点O处的电势为2V,与c点的电势相等,以O点为圆心做三角形的外接圆,连接圆心O和c,并通过b、a两点分别作Oc的平行线,因为Oa=Ob=Oc=R,所以三条平行线是等势差的.再过O点作三条平行线的垂线,交三角形abc的外接圆于d、e两点,则d.点电势最高,e点电势最低.由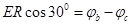 ,
,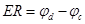 ,
,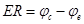 且
且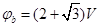 , φc=2 V解得
, φc=2 V解得 ,
,  ,所以B正确,ACD.均错误.
,所以B正确,ACD.均错误.
思路分析:作出三角形的外接圆,其圆心O在ab的中点,该点电势为2V,OC为等势线,作出OC的垂线MN为电场线,根据U=Ed,顺着电场线MN,找出离O点最远的点,电势最低;逆着电场线,离O点最远点电势最高.
试题点评:找等势点,作等势线,进一步作出电场线,并结合几何知识是求电势问题常用的方法.

练习册系列答案
相关题目
 如图所示,在匀强电场中有a、b、c三点,a、b相距 5cm,b、c相距12cm.将一个带电荷量为4×10-8C 的电荷从a点移到b点时,电场力做功为1.2×10-7 J.
如图所示,在匀强电场中有a、b、c三点,a、b相距 5cm,b、c相距12cm.将一个带电荷量为4×10-8C 的电荷从a点移到b点时,电场力做功为1.2×10-7 J. 如图所示,在匀强电场中有A、B、C三点,在以它们为顶点的三角形中,∠A=30°,∠C=90°,电场方向与三角形所在平面平行.已知A、B、C三点的电势分别为(
如图所示,在匀强电场中有A、B、C三点,在以它们为顶点的三角形中,∠A=30°,∠C=90°,电场方向与三角形所在平面平行.已知A、B、C三点的电势分别为( 如图所示,在匀强电场中有A、B两个带电粒子,电荷量分别为q和2q,质量分别为m和4m,两粒子重力不计,分别从A点由静止释放到达B点时,它们的速度大小之比为多少?
如图所示,在匀强电场中有A、B两个带电粒子,电荷量分别为q和2q,质量分别为m和4m,两粒子重力不计,分别从A点由静止释放到达B点时,它们的速度大小之比为多少? 如图所示,在匀强电场中有a,b,c三点,这三点连线组成一个直角三角形,ab边和电场线平行,长为3cm,a点离A板1cm,电源电压为2V,B板接地.问:
如图所示,在匀强电场中有a,b,c三点,这三点连线组成一个直角三角形,ab边和电场线平行,长为3cm,a点离A板1cm,电源电压为2V,B板接地.问: 匀强电场中有A、B、C三点,连线成一个直角三角形,其所在平面与电场线平行AB=5cm,AC=4cm,把一个电荷量为-2×10-9C的点电荷从A移到C,静电力做功8×10-9J,从C沿BC移到B,静电力不做功,
匀强电场中有A、B、C三点,连线成一个直角三角形,其所在平面与电场线平行AB=5cm,AC=4cm,把一个电荷量为-2×10-9C的点电荷从A移到C,静电力做功8×10-9J,从C沿BC移到B,静电力不做功,