题目内容
2．
如图所示，光滑水平面上停有一辆带支架的小车，支架上用细绳悬挂一个小球，当小球从最左端的A点相对小车由静止开始摆动到最右端的B点的过程中，下列说中正确的是（ ）| A． | 小球的机械能不守恒 | |
| B． | 从A摆动到最低点O的过程中，细绳对小球做负功 | |
| C． | 从最低点O摆到B的过程中，细绳对小车做负功 | |
| D． | A、B两点应在同一水平线上 |
分析 根据机械能守恒的条件：只有重力做功（对单个物体而言），分析小球的机械能是否守恒．判断一个力做功的正负关键看力的方向和速度方向的夹角，夹角小于90°做正功，夹角大于90°做负功，等于90°不做功．
解答 解：A、当小球摆动时，车子在绳子拉力作用下会向反方向移动，则绳子的拉力与小球的速度（对地速度）不垂直，则绳子拉力对小球做功，则小球的机械能不守恒，故A正确．
B、从A摆动到最低点O的过程中，小车向左移动，小球对地的瞬时速度将与绳子不垂直，夹角大于90°，故细绳对小球做负功，故B正确．
C、从最低点O摆到B的过程中，细绳的拉力与小车瞬时速度的夹角大于90°，则细绳的拉力对小车做负功，故C正确．
D、由于车和球这个系统水平方向上动量守恒，可知，A、B两点时，系统的动能为零，由系统的机械能守恒可知，A、B两点在同一高度，即在同一水平线上，故D正确；
故选：ABCD
点评 本题的关键要掌握判断一个力做功正负的方法，要注意对整体应用动量守恒定律及功能关系进行分析．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
18．小明同学用玩具手枪研究平抛运动的规律．已知枪口离地面的高度为h1，枪口与竖直墙的距离为S，重力加速度为g，水平射出的子弹大在墙上的点离地面的高度为h2．则子弹射出时的初速度为（ ）
| A． | S$\sqrt{\frac{g}{2（{h}_{1}-{h}_{2}）}}$ | B． | S$\sqrt{\frac{g}{2{h}_{1}}}$ | C． | S$\sqrt{\frac{g}{2{h}_{2}}}$ | D． | S$\sqrt{\frac{2{h}_{1}}{g}}$ |
19．甲、乙两星球的平均密度相等，半径之比是R甲：R乙=4：1，则同一物体在这两个星球表面受到的重力之比是（ ）
| A． | 1：1 | B． | 4：1 | C． | 1：16 | D． | 1：64 |
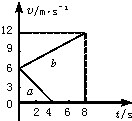质量为0.8kg的物体在一水平面上运动，如图所示的两条直线分别表示物体受到水平拉力作用和不受拉力作用的v-t图线．则图线b（填“a”或“b”）表示物体受拉力作用时的运动，该物体所受到的拉力是1.8N．
3．关于加速度，下列说法正确的是（ ）
| A． | 加速度就是增加出来的速度 | B． | 加速度增大，速度一定增大 | ||
| C． | 速度变化量越大，加速度就越大 | D． | 加速度为负值，速度可能增大 |
利用图示的装置来测量滑块A在长木板上运动的加速度．图中d为安装在滑块A上挡光片的宽度，s是1和2两个光电门之间的距离．实验时，使滑块A从长木板的顶端滑下．
