��Ŀ����
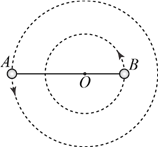
����Ŀ����ͼ��ʾ���뾶ΪR�İ�Բ���۹̶���ˮƽ���ϣ��ۿ����ϣ��ۿ�ֱ��ˮƽ��һ������Ϊm������P���ɾ�ֹ�ͷŸպôӲۿ�A������ײ�ؽ�����У�����Բ���������ʵػ��е�B�㣬�������Ĵ�С��P�㵽A��߶�Ϊh���������ٶȴ�СΪg��������˵����ȷ����

A.����P��B���̿˷�Ħ�������Ĺ�Ϊmg(R+h)
B.����A��B������Բ���ۼ���ѹ��Ϊ![]()
C.�����B��ʱ�Բ۵�ѹ����СΪ![]()
D.��鵽B��ʱ������˲ʱ����Ϊmg![]()
���𰸡�C
��������
A������![]() ��
��![]() ������Բ���˶������ܲ��䣬�ɶ��ܶ����ã�
������Բ���˶������ܲ��䣬�ɶ��ܶ����ã�
![]()
�ɵ�����![]() ��
��![]() ���̿˷�Ħ�������Ĺ�Ϊ��
���̿˷�Ħ�������Ĺ�Ϊ��
![]()
��������![]() ��
��![]() ���̿˷�Ħ�������Ĺ�Ϊ
���̿˷�Ħ�������Ĺ�Ϊ![]() ����A����
����A����
B������![]() ��
��![]() �Ĺ��̣��ɻ�е���غ�ã�
�Ĺ��̣��ɻ�е���غ�ã�
![]()
�ɵ���鵽��![]() ����ٶȴ�СΪ��
����ٶȴ�СΪ��
![]()
������![]() ��
��![]() ���̣�Բ���۶�����֧����Ϊ
���̣�Բ���۶�����֧����Ϊ![]() ��Բ���۶�����֧��������ֱ����ļн�Ϊ
��Բ���۶�����֧��������ֱ����ļн�Ϊ![]() ����ţ�ٵڶ����ɵã�
����ţ�ٵڶ����ɵã�
![]()
����ţ�ٵ������ɿɵ�����![]() ��
��![]() ������Բ���ۼ���ѹ��Ϊ��
������Բ���ۼ���ѹ��Ϊ��
![]()
��B����
C�������![]() ��ʱ����ţ�ٵڶ����ɵã�
��ʱ����ţ�ٵڶ����ɵã�
![]()
�ɵã�
![]()
����ţ�ٵ�������֪�����![]() ��ʱ�Բ۵�ѹ����СΪ
��ʱ�Բ۵�ѹ����СΪ![]() ����C��ȷ��
����C��ȷ��
D����鵽![]() ��ʱ�������ٶȴ�ֱ�����������˲ʱ����Ϊ�㣬��D����
��ʱ�������ٶȴ�ֱ�����������˲ʱ����Ϊ�㣬��D����
��ѡC��

��ϰ��ϵ�д�
�����Ŀ