Question

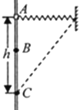
【题目】静止在水平地面上的两小物块A、B，质量分别为，；两者之间有一被压缩的微型弹簧，A与其右侧的竖直墙壁距离l=1.0m，如图所示，某时刻，将压缩的微型弹簧释放，使A、B瞬间分离，两物块获得的动能之和为，释放后，A沿着与墙壁垂直的方向向右运动。A、B与地面之间的动摩擦因数均为，重力加速度取，A、B运动过程中所涉及的碰撞均为弹性碰撞且碰撞时间极短。

(1)求弹簧释放后瞬间A、B速度的大小；

(2)物块A、B中的哪一个先停止？该物块刚停止时A与B之间的距离是多少？

(3)A和B能否再次发生碰撞？若不能，说明理由；若能，试计算碰后的速度大小。

Answer 1

【答案】(1)，；(2)B，0.50m；(3)不能，见解析

【解析】

(1)设弹簧释放瞬间A和B的速度大小分别为、，以向右为正，由动量守恒定律和题给条件有

联立并代入题给数据得

(2)A、B两物块与地面间的动摩擦因数相等，因而两者滑动时加速度大小相等，设加速度大小为，则有

假设A和B发生碰撞前，已经有一个物块停止，此物块应为弹簧释放后速度较小的B，设从弹簧释放到B停止所需时间为，B向左运动的路程为，则有

可得

在时间内，A可能与墙发生弹性碰撞，碰撞后A将向左运动，碰撞并不改变A的速度大小，所以无论此碰撞是否发生，A在时间内的路程都可表示为

这表明在时间内A已与墙壁发生碰撞，但没有与B发生碰撞，此时A位于出发点右边0.25 m处，B位于出发点左边0.25 m处，两物块之间的距离为

(3)时刻后A将继续向左运动，假设它能与静止的B碰撞，碰撞时速度的大小为，由动能定理有

可得

故A与B将发生碰撞，设碰撞后A、B的速度分别为以和，规定以向右为正，由动量守恒定律与机械能守恒定律有

联立并代入题给数据得

这表明碰撞后A将向右运动，B继续向左运动，设碰撞后A向运动距离为时停止，B向左运动距离为时停止，由动能定理可得

代入数据得

则有

所以A和B不能再次发生碰撞