题目内容
如图所示，质量为15kg的物体用两根绳子AO和BO吊挂在天花板下处于静止状态，绳AO、BO与竖直方向的夹角分别为53°、37°．（sin37°=0.6，cos37°=0.8，取g=10m/s2）（1）求两根绳子受到的拉力大小．
（2）如果绳AO、BO的最大承受力都是200N，为了使绳子不被拉断，则所挂的重物的质量最多不能超过多少？
分析：（1）以结点O为研究对象，将重物的拉力按照作用效果进行分解，求解两个分力，等于两个绳子的拉力；
（2）假设在绳子均不被拉断的情况下，分别求出轻绳AO、BO所能承受的拉力达到最大时重物的质量，再确定重物的最大质量．
（2）假设在绳子均不被拉断的情况下，分别求出轻绳AO、BO所能承受的拉力达到最大时重物的质量，再确定重物的最大质量．
解答：解：（1）将重物对O点的拉力按照作用效果分解，如图所示：
解得：
F1=Gcos37°=0.8mg=0.8×150N=120N
F2=Gsin37°=0.6mg=0.6×150N=90N
故AO绳子的拉力为90N，BO绳子的拉力为120N；
（2）由于：
F1=Gcos37°=0.8mg
F2=Gsin37°=0.6mg
当AO绳子的拉力F2为200N时，BO绳子的拉力1为
mg=267N＞200N，BO绳子已断；
当BO绳子的拉力F1为200N时，AO绳子的拉力2为
mg=150N＜200N，AO绳子没有断，此时物体的质量为：
m=
=
=25kg；
答：（1）AO绳子的拉力为90N，BO绳子的拉力为120N；
（2）如果绳AO、BO的最大承受力都是200N，为了使绳子不被拉断，则所挂的重物的质量最多不能超过25kg．
解得：
F1=Gcos37°=0.8mg=0.8×150N=120N
F2=Gsin37°=0.6mg=0.6×150N=90N
故AO绳子的拉力为90N，BO绳子的拉力为120N；
（2）由于：
F1=Gcos37°=0.8mg
F2=Gsin37°=0.6mg
当AO绳子的拉力F2为200N时，BO绳子的拉力1为
| 4 |
| 3 |
当BO绳子的拉力F1为200N时，AO绳子的拉力2为
| 3 |
| 4 |
m=
| 200 |
| gcos37° |
| 200 |
| 10×0.8 |
答：（1）AO绳子的拉力为90N，BO绳子的拉力为120N；
（2）如果绳AO、BO的最大承受力都是200N，为了使绳子不被拉断，则所挂的重物的质量最多不能超过25kg．
点评：本题是物体平衡中临界问题，采用的是假设法．其基础是分析物体受力、正确作出力的分解图．
练习册系列答案
相关题目
如图所示，质量为M的斜劈倾角为θ，在水平面上保持静止，当将一质量为m的木块放在斜面上时正好匀速下滑．如果用与斜面成α角的力F拉着木块沿斜面匀速上滑．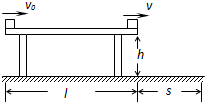
如图所示，质量为m的小物块A在粗糙水平桌面上做直线运动，经距离l后与质量为m的小物块B发生碰撞，并粘在一起以速度v飞离桌面，最终落在水平地面上．已知l=3.0m，v=2.0m/s，m=0.10kg，物块与桌面间的动摩擦因数μ=0.15，桌面高h=0.45m．不计空气阻力，重力加速度g取10m/s2．求
如图所示，质量为M=1kg木板静止在水平面上，一质量为m=1kg的滑块以5m/s 的水平初速度从右端滑上木板，最终静止在木板上．滑块与木板间动摩擦因数μ1=0.4，木板与水平面间的动摩擦因数μ2=0.15，取g=10m/s2，求：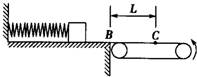
如图所示，质量为m=1kg的滑块，放在光滑的水平平台上，平台的右端B与足够长的水平传送带相接，皮带轮的半径为R=o.5m，且以角速度ω=12rad/s逆时针转动（传送带不打滑），先将滑块缓慢向左压缩固定在平台上的轻弹簧，然后突然释放，当滑块滑到传送带上距B端L=15m的C点时，与传送带速度大小相等，滑块与传送带之间的动摩擦因数μ=0.15．（g=10m/s2）求：