题目内容
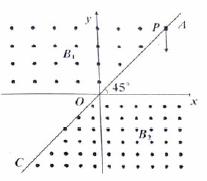
如图所示，直角坐标平面xOy内有一条直线AC过坐标原点O与x轴成45°夹角，在OA与x轴负半轴之间的区域内存在垂直xOy平面向外的匀强磁场B，在OC与x轴正半轴之间的区域内存在垂直xOy平面向外的匀强磁场B2。现有一质量为m，带电量为q（q>0）的带电粒子以速度v从位于直线AC
上的P点，坐标为（L，L），竖直向下射出，经测量发现，此带电粒子每经过相同的时间T，会再将回到P点，已知距感应强度
。（不计粒子重力）
（1）请在图中画出带电
粒子的运动轨迹，并求出匀强磁场B1与B2的比值；（B1、B2磁场足够大）
（2）求出带电粒子相邻两次经过P点的时间间隔T；
（3）若保持磁感应强度B2不变，改变B1的大小，但不改变其方向，使
。现从P点向下先后发射速度分别为
的与原来相同的带电粒子（不计两个带电粒子之间的相互作用力，并且此时算作第一次经过直线AC），如果它们第三次经过直线AC时轨迹与AC的交点分别 记为E点和F点（图中未画出），试求EF两点间的距离。
（4）若要使（3）中所说的两个带电粒子同时第三次经过直线AC，问两带电粒子第一次从P点射出时的时间间隔△t要多长？
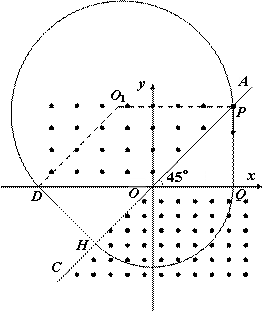
解答：（1）(6分)带电粒子从P点匀速运动到Q点，然后作半径为：
的匀速圆周运动，运动到H点时的速度方向与AC垂直，从H点匀速运动到D点，后作匀速圆周运动到P点。根据平面几何知识可知：
，四边形AODOR1R为棱形，OR1R为圆心，即带电粒子在匀强磁场BR1R中作匀速圆周运动时的半径RR1R为
，根据
，得：
（2）(5分)
，
，
，
（3）(6分)两带电粒子在磁场BR2R中运动时的半径为：
，
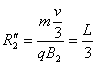
，故粒子在磁场BR1R中的运动半径
，则两带电粒子都刚好运动1／4圆周到达A点，所以：EF两点间的距离EF=0（如图所示）
（4）(5分)两带电粒子在同一磁场中的周期相同，转过的圆心角也相同，故在同一磁场中的运动时间相同，所以时间间隔Δt就是直线运动的时间差：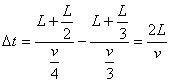
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
在“研究平抛物体的运动”的实验中：
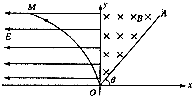如图所示，在直角坐标平面的第I象限内有一匀强磁场区域，磁感应强度为B，直线OA是磁场右侧的边界．在第Ⅱ象限区域，存在电场强度大小为E的水平向左的匀强电场，y轴是电场、磁场区域的分界线曲线，OM满足方程x=-ky2（k＞0）．有一带电荷量为q、质量为m的负粒子（重力不计）在曲线OM上某一点由静止释放，穿越y轴进入磁场中．
，立即在第一象限内再加垂直于Oxy平面向里的匀强磁场(图中未画出)，磁感应强度为
，再经过时间to，=撤去匀强磁场。已知E1=
，E2=
，细线能够承受的最大拉力是F0=3mg。(结果用g、L、m表示)求：