��Ŀ����
5�� ��ͼ������ΪM=72kg�����������ˮƽ�����ϣ����������쳤����������⻬���ʻ��֣���һ�����������һ�˱�����Ϊm=60kg����ץס���������ǡ�ô�����ֱ����״̬����ͨ��ץ����a=4m/s2�ļ��ٶ���ֱ����2m��gȡ10m/s2����˹��̣�������
��ͼ������ΪM=72kg�����������ˮƽ�����ϣ����������쳤����������⻬���ʻ��֣���һ�����������һ�˱�����Ϊm=60kg����ץס���������ǡ�ô�����ֱ����״̬����ͨ��ץ����a=4m/s2�ļ��ٶ���ֱ����2m��gȡ10m/s2����˹��̣�������| A�� | ����ļ��ٶ�Ϊ2m/s2 | B�� | ���ӵ�����Ϊ840N | ||
| C�� | �˵�����������Ϊ2380J | D�� | ����������������ƽ������Ϊ700W |
���� ���˺������������������ţ�ٵڶ�������ü��ٶȣ������˶�ѧ��ʽ��û�õ��ٶȺ�ͨ����λ�ƣ�������ݶ��ܶ�������˵���������
��� �⣺A������������������F-mg=ma�����F=mg+ma=840N�����������ţ�ٵڶ����ɿ�֪��F-Mg=Ma�䣬���$a��=\frac{5}{3}m/{s}^{2}$����A����B��ȷ��
C������2m�˻�õ��ٶ�v=$\sqrt{2ah}=4m/s$��������ʱ��t=$\frac{v}{a}=1s$�����������ĸ߶�$h��=\frac{1}{2}a��{t}^{2}=\frac{5}{6}m$����õ��ٶ�v$��=a��t=\frac{5}{3}m/s$
���˺�������ɵ����壬���ݶ��ܶ�����֪$W-mgh-Mgh��=\frac{1}{2}m{v}^{2}+\frac{1}{2}Mv{��}^{2}$�����W=2380J����C��ȷ��
D����������������W=Mgh�䣬ƽ������P=$\frac{W}{t}=700W$����D��ȷ
��ѡ��BCD
���� ������Ҫ������ţ�ٵڶ����ɺ��˶�ѧ��ʽ������Cѡ���ǣ����˺�������Ϊ�������ö��ܶ����������

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
16��������Ȼ�����ԣ�����˵����ȷ���ǣ�������
| A�� | ����Ԫ�ض����ܷ���˥�� | |
| B�� | ������Ԫ�صİ�˥���������¶��й� | |
| C�� | ��������Ԫ������Ԫ���γɻ�����ʱ���������ʧ | |
| D�� | �����ºͦ����������У������ߵĴ�������ǿ |
10�� ��ͼ��ʾ������ƽ�н���������ˮƽ��ɦȽǹ̶����ã������һ����ֵ����R������Ϊm�Ĺ⻬�������������챣�ִ�ֱ���Ӵ����ã�������������ĵ�����ɺ��Բ��ƣ�����װ�ô����뵼��ƽ�洹ֱ����ǿ�ų��У��������ܵ�ƽ�е������ϵĺ���F�������ϼ����˶�����һС��ʱ���ڣ�������
��ͼ��ʾ������ƽ�н���������ˮƽ��ɦȽǹ̶����ã������һ����ֵ����R������Ϊm�Ĺ⻬�������������챣�ִ�ֱ���Ӵ����ã�������������ĵ�����ɺ��Բ��ƣ�����װ�ô����뵼��ƽ�洹ֱ����ǿ�ų��У��������ܵ�ƽ�е������ϵĺ���F�������ϼ����˶�����һС��ʱ���ڣ�������
 ��ͼ��ʾ������ƽ�н���������ˮƽ��ɦȽǹ̶����ã������һ����ֵ����R������Ϊm�Ĺ⻬�������������챣�ִ�ֱ���Ӵ����ã�������������ĵ�����ɺ��Բ��ƣ�����װ�ô����뵼��ƽ�洹ֱ����ǿ�ų��У��������ܵ�ƽ�е������ϵĺ���F�������ϼ����˶�����һС��ʱ���ڣ�������
��ͼ��ʾ������ƽ�н���������ˮƽ��ɦȽǹ̶����ã������һ����ֵ����R������Ϊm�Ĺ⻬�������������챣�ִ�ֱ���Ӵ����ã�������������ĵ�����ɺ��Բ��ƣ�����װ�ô����뵼��ƽ�洹ֱ����ǿ�ų��У��������ܵ�ƽ�е������ϵĺ���F�������ϼ����˶�����һС��ʱ���ڣ�������| A�� | F������mg�ĺ��������Ĺ����ڵ���R�ϲ����Ľ����� | |
| B�� | F�Ͱ������ĺ��������Ĺ����ڽ�������е�ܵ����� | |
| C�� | F�����Ĺ����ڽ������������ܵ��������͵���R�ϲ����Ľ�����֮�� | |
| D�� | �����ڽ������ϵĺ��������Ĺ����ڵ���R�ϲ����Ľ����� |
4����ͼ��ʾ�����ΪL�������㹻����ƽ�н�������MN��PQ���������һƽ�а��������ƽ�а��������������ֱ���ã�����ľ���Ϊd������������֮�仹������һ������R������װ�ñ��̶���ˮƽ�����ϣ�������AB������Ϊm������Ϊr����ֱ���ڵ����ϣ��������������͵������������������ռ���ڴ�ֱ�ڵ���ƽ�����ϵ���ǿ�ų����Ÿ�Ӧǿ�ȴ�С��ΪB�����ڸ�������AB ʩ��һˮƽ���ҵ���������ʹ������AB�����˶�����һ���������������������ٶ�v0ƽ�е��������������������ǡ����ֱ���˶���������˵����ȷ���ǣ�������


| A�� | �����ڽ�����ABˮƽ���ҵ���F=$\frac{{B}^{2}Ld{v}_{0}}{R}$ | |
| B�� | ������AB���ٶ�v=$\frac{d��R+r��}{LR}$v0 | |
| C�� | ����R�ϵĵ繦��P=$\frac{{B}^{2}{d}^{2}{{v}_{0}}^{2}��R+r��}{{R}^{2}}$ | |
| D�� | ��ʱ��t�ڽ�����AB�ϵIJ���������Q=$\frac{{B}^{2}{d}^{2}{{v}_{0}}^{2}rt}{{R}^{2}}$ |
 ��ͼ��ʾ��һ����Ϊm�������Ϊq�Ĵ������Ӵ�ƽ��ֱ������ϵy���ϵ�A����������������������ǿ�糡����ǿ�ų��У����ӽ�����������ٶ�Ϊv������y���30��ǵ�ֱ���˶��������һ���ޣ������һ����ų����䣬���糡�ɵ���������ˮƽ���ҵ���ǿ�糡E1��Ϊ��ֱ���ϵ���ǿ�糡E2����Բ�ι켣�˶�һ�κ��y���ϵ�C��ˮƽ����ڶ����ޣ��ڶ�����������û�дų����糡���һ���ȴ�����֪�������ٶ�Ϊg����
��ͼ��ʾ��һ����Ϊm�������Ϊq�Ĵ������Ӵ�ƽ��ֱ������ϵy���ϵ�A����������������������ǿ�糡����ǿ�ų��У����ӽ�����������ٶ�Ϊv������y���30��ǵ�ֱ���˶��������һ���ޣ������һ����ų����䣬���糡�ɵ���������ˮƽ���ҵ���ǿ�糡E1��Ϊ��ֱ���ϵ���ǿ�糡E2����Բ�ι켣�˶�һ�κ��y���ϵ�C��ˮƽ����ڶ����ޣ��ڶ�����������û�дų����糡���һ���ȴ�����֪�������ٶ�Ϊg���� ŷķ���ڲ���·����ͼ��ʾ����Դ����r=1.0������������ƫ����Ig=10mA������������Rg=9.0����A��BΪ��������
ŷķ���ڲ���·����ͼ��ʾ����Դ����r=1.0������������ƫ����Ig=10mA������������Rg=9.0����A��BΪ�������� ��ͼ��ʾ����������=200nm�����������䵽������ʱ���ݳ��Ĺ������������E=3.5eV����֪���ʿ˳���h=6.6��10-34J•s����������еĴ����ٶ�c=3.0��108m/s����
��ͼ��ʾ����������=200nm�����������䵽������ʱ���ݳ��Ĺ������������E=3.5eV����֪���ʿ˳���h=6.6��10-34J•s����������еĴ����ٶ�c=3.0��108m/s���� ��ͼ��ʾ���о���Ÿ�Ӧ�����ʵ�����������߿��ڸ�����ԭ����Ȧ���ߵ��Ʒ���ʵ��ǰ�Ѳ����������е����������������ʱָ������ƫ��
��ͼ��ʾ���о���Ÿ�Ӧ�����ʵ�����������߿��ڸ�����ԭ����Ȧ���ߵ��Ʒ���ʵ��ǰ�Ѳ����������е����������������ʱָ������ƫ��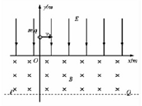 ��ͼ��ʾ����ֱ������ϵ�ĵ�һ���������д�����y�Ḻ�������ǿ�糡���糡ǿ�ȴ�СΪE���ڵ������������д����ſ���δ֪�Ĵ�ֱֽ���������ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB��x�������ϱ߽磬�±߽���x��ƽ�е�����PQ��һ����Ϊm��������Ϊ+q�����ӣ���������������y���ϣ�0��y0��λ���Գ��ٶ�v0��x��������������ǿ�糡��
��ͼ��ʾ����ֱ������ϵ�ĵ�һ���������д�����y�Ḻ�������ǿ�糡���糡ǿ�ȴ�СΪE���ڵ������������д����ſ���δ֪�Ĵ�ֱֽ���������ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB��x�������ϱ߽磬�±߽���x��ƽ�е�����PQ��һ����Ϊm��������Ϊ+q�����ӣ���������������y���ϣ�0��y0��λ���Գ��ٶ�v0��x��������������ǿ�糡��