题目内容
一倾角为θ=45°的斜面固定于地面，斜面顶端离地面的高度h0=1m，斜面底端有一垂直于斜面的固定挡板，在斜面顶端自由释放一质量m=0.09 kg的小物块（视为质点）。小物块与斜面之间的动摩擦因数μ=0.2，当小物块与挡板碰撞后，将以原速返回。重力加速度g=10 m/s2。在小物块与挡板的前4次碰撞过程中，挡板给予小物块的总冲量是多少？
解：设小物块从高为h处由静止开始沿斜面向下运动，到达斜面底端时速度为v
由功能关系得
①
以沿斜面向上为动量的正方向。按动量定理，碰撞过程中挡板给小物块的冲量I=mv-m(-v) ②
设碰撞后小物块所能达到的最大高度为h'，则
③
同理，有
④
I'=mv'-m(-v') ⑤
式中，v'为小物块再次到达斜面底端时的速度，I'为再次碰撞过程中挡板给小物块的冲量
由①②③④⑤式得I'=kI ⑥
式中
⑦
由此可知，小物块前4次与挡板碰撞所获得的冲量成等比级数，首项为
⑧
总冲量为I=I1+I2+I3+I4=I1(1+k+k2+k3) ⑨
由
⑩
得
代入数据得
由功能关系得
① 以沿斜面向上为动量的正方向。按动量定理，碰撞过程中挡板给小物块的冲量I=mv-m(-v) ②
设碰撞后小物块所能达到的最大高度为h'，则
③ 同理，有
④I'=mv'-m(-v') ⑤
式中，v'为小物块再次到达斜面底端时的速度，I'为再次碰撞过程中挡板给小物块的冲量
由①②③④⑤式得I'=kI ⑥
式中
⑦ 由此可知，小物块前4次与挡板碰撞所获得的冲量成等比级数，首项为
⑧ 总冲量为I=I1+I2+I3+I4=I1(1+k+k2+k3) ⑨
由
⑩ 得
代入数据得
练习册系列答案
相关题目
如图所示，一倾角为45°的斜面固定于竖直墙上，为使一光滑的铁球静止，需加一水平力F，且F过球心，下列说法正确的是（ ）
如图所示，一倾角为45°的斜面固定于竖直墙上，为使一光滑匀质铁球静止，需加一水平力F，若力F过球心，下列说法中正确的是（ ）| A、球一定受墙的弹力且水平向左 | B、球可能受墙的弹力且水平向左 | C、球一定受斜面的弹力且垂直斜面向上 | D、球一定同时受到墙的弹力和斜面的弹力 |
（2008?四川）一倾角为θ=45°的斜面固定于地面，斜面顶端离地面的高度h0=1m，斜面底端有一垂直于斜面的固定挡板．在斜面顶端自由释放一质量m=0.09kg的小物块（视为质点）．小物块与斜面之间的动摩擦因数μ=0.2．当小物块与挡板碰撞后，将以原速返回．重力加速度g=10m/s2．在小物块与挡板的前4次碰撞过程中，挡板给予小物块的总冲量是多少？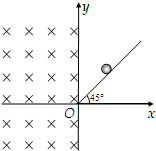
（2011?株洲二模）如图，竖直平面内有一直角坐标系xOy，在x≥0的区域内有一倾角为45°的绝缘光滑斜面，斜面末端O处用一极小的平滑曲面连接，恰能使斜面末端水平．在x≤0的广泛区域内存在正交的匀强磁场和匀强电场，磁场垂直于纸面向里，磁感应强度大小为B；电场沿竖直方向，场强大小为E．电荷量为-q的带电小球从绝缘光滑斜面上某点由静止开始下滑，小球经斜面末端O点进入电场和磁场，之后沿圆周运动，垂直于y轴离开电场和磁场，最后垂直打到斜面上．