题目内容
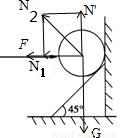
如图所示,一个倾角为45°的斜面固定于竖直墙上,为使一光滑的铁球静止在如图所示的位置,需用一个水平推力F作用于球体上,F的作用线通过球心。设球体的重力为G,竖直墙对球体的弹力为N1,斜面对球体的弹力为N2 ,则以下结论正确的是

A.N1=F B.G≤F C.N2>G D.N2>N1
【答案】
BC
【解析】
试题分析:如图所示,小球受重力、推力、斜面的支持力及竖直墙的支持力;将斜面的支持力进行分解为竖直方向上的N′=N2cos45°、水平向上的N″=N2sin45°,则由共点力的平衡条件可知:水平方向上:F=N1+N″=N1+N2sin45°;故F一定大于N1;故A错误;竖直方向上:G=N/=N2cos45°,故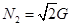 ,故N2>G,故C正确;联立两式可得:G=F-N1;故G<F;若压力F等于N2水平向上的分力时,小球有可能对竖直面没有压力,故N1有可能为零,故G可以等于F;故G≤F,故B正确;由以上分析可知,物体的平衡关系无法判断N1、N2的大小关系,故D错误;故选B、C.
,故N2>G,故C正确;联立两式可得:G=F-N1;故G<F;若压力F等于N2水平向上的分力时,小球有可能对竖直面没有压力,故N1有可能为零,故G可以等于F;故G≤F,故B正确;由以上分析可知,物体的平衡关系无法判断N1、N2的大小关系,故D错误;故选B、C.
考点:共点力的平衡问题。

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 如图所示,一个倾角为θ的斜面固定在水平地面上,质量为m的物块与斜面之间的动摩擦因数为μ.并以某一初速度沿劈的斜面向上滑,至速度为零后静止在斜面上.则下列选项中正确的是( )
如图所示,一个倾角为θ的斜面固定在水平地面上,质量为m的物块与斜面之间的动摩擦因数为μ.并以某一初速度沿劈的斜面向上滑,至速度为零后静止在斜面上.则下列选项中正确的是( )| A、物块在上滑过程中所受摩擦力大小为mgsinθ | B、物块在上滑过程中所受摩擦力大小为μmg | C、物块m静止在斜面上后,所受的摩擦力大小为μmgcosθ | D、物块m静止在斜面上后,所受的摩擦力大小为mgsinθ |
 如图所示,一个倾角为θ的光滑斜面,固定在光滑竖直墙壁上,为使质量为m的铁球静止于墙壁与斜面之间,水平推力F作用在球上,F至少多大?斜面受到铁球的压力多大?
如图所示,一个倾角为θ的光滑斜面,固定在光滑竖直墙壁上,为使质量为m的铁球静止于墙壁与斜面之间,水平推力F作用在球上,F至少多大?斜面受到铁球的压力多大? (1)如图所示,一个倾角为θ的斜面上,放一个重G的光滑小球,球被竖直的挡板挡住,则斜面对球的支持力的大小是多少?竖直的挡板对球的弹力是多少?
(1)如图所示,一个倾角为θ的斜面上,放一个重G的光滑小球,球被竖直的挡板挡住,则斜面对球的支持力的大小是多少?竖直的挡板对球的弹力是多少? 如图所示,一个倾角为θ的木楔固定在水平地面上,在其斜面上放有一个质量为m的小物块,整个装置处于静止状态.那么,在某段时间t内木楔的斜面对小物块的冲量的大小和方向是( )
如图所示,一个倾角为θ的木楔固定在水平地面上,在其斜面上放有一个质量为m的小物块,整个装置处于静止状态.那么,在某段时间t内木楔的斜面对小物块的冲量的大小和方向是( ) 如图所示,一个倾角为α的光滑斜面上,宽度为L的区域中,有垂直斜面方向的匀强磁场,磁感应强度大小为B.将-个质量为m、电阻为Ω、边长为a的闭合正方形金属框.沿斜面以某一速度匀速地通过磁场区域,在金属框进入磁场区域到穿出磁场区域过程中外力做功为W,求金属框的速度大小?
如图所示,一个倾角为α的光滑斜面上,宽度为L的区域中,有垂直斜面方向的匀强磁场,磁感应强度大小为B.将-个质量为m、电阻为Ω、边长为a的闭合正方形金属框.沿斜面以某一速度匀速地通过磁场区域,在金属框进入磁场区域到穿出磁场区域过程中外力做功为W,求金属框的速度大小?