题目内容
（2009?淮南三模）如图所示，在长方形区域（虚线框）内有一垂直于纸面向外的匀强磁场，一束质子以不同的速度从O点沿着图示的方向射入磁场后，分别从a、b、c、d四个点射出磁场，下列关于它们在磁场中的运动时间的比较中，正确的是（ ）分析：质子进入匀强磁场后只受洛伦兹力做匀速圆周运动，四个质子运动的周期都相同，作出轨迹，根据圆心角的大小判断质子在磁场运动时间的大小．
解答：
解：质子在匀强磁场中做匀速圆周运动的周期为
T=
四个质子m、q相同，B也相同，则它们圆周运动的周期相同．
画出质子运动的轨迹如图．从图1看出，从a、b两点射出的质子轨迹所对的圆心角都是π，
则tA=tB=
T=
T
从图2看出，从d射出的质子轨迹所对的圆心角∠OO2d＜∠OO1C＜π，
根据圆周运动的时间t=
T，T相同时，圆心角α越大，时间t越大，所以
＞tC＞tD．所以tA=tB＞tC＞tD．故D正确，ABC错误；
故选：D．
解：质子在匀强磁场中做匀速圆周运动的周期为T=
| 2πm |
| Bq |
四个质子m、q相同，B也相同，则它们圆周运动的周期相同．
画出质子运动的轨迹如图．从图1看出，从a、b两点射出的质子轨迹所对的圆心角都是π，
则tA=tB=
| π |
| 2π |
| 1 |
| 2 |
从图2看出，从d射出的质子轨迹所对的圆心角∠OO2d＜∠OO1C＜π，
根据圆周运动的时间t=
| α |
| 2π |
| T |
| 2 |
故选：D．
点评：带电粒子在匀强磁场中做匀速圆周运动的问题，画轨迹是基本方法，也是基本能力，注意：粒子运动的时间常常根据t=
T（α是轨迹的圆心角）求解．
| α |
| 2π |
练习册系列答案
相关题目
（2009?淮南三模）在竖直平面内，有根光滑金属杆弯成如图所示形状，相应的曲线方程为y=Acosx，将一个光滑小环套在该金属杆上，并从x=0、y=A处以某一初速度沿杆向+x方向运动．运动过程中（ ）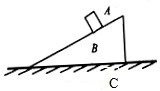
（2009?淮南三模）如图所示，物块A沿楔形块B的斜面下滑时，B相对于水平地面C静止不动，设A、B间的动摩擦因数为μ1，B、C间的动摩擦因数为μ2，则下列说法中不可能的是（ ）
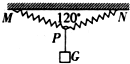（2009?淮南三模）如图所示，原长为l、劲度系数为k的轻弹簧固定于同一高度的M、N两点，在弹簧的中点P处悬挂一重为G的物体，整个装置处于平衡，此时MP与PN之间的夹角为120°，则此时弹簧的总长度为（ ）