题目内容
7.一只爆竹竖直升空后,在距离地面高为h处到达最高点,发生爆炸,分为质量不同的两块,两块的质量之比2:1,其中质量较小的一块获得的水平速度大小为v,则两块爆竹落地后相距( )| A. | 2v$\sqrt{\frac{2h}{g}}$ | B. | v$\sqrt{\frac{2h}{g}}$ | C. | $\frac{3v}{2}$$\sqrt{\frac{2h}{g}}$ | D. | $\frac{2v}{3}$$\sqrt{\frac{2h}{g}}$ |
分析 根据两块爆竹爆炸时水平方向动量守恒求出大块爆竹的速度,然后根据平抛运动求出时间和水平位移.
解答 解:设其中一块质量为m,则另一块质量为2m,
爆炸过程系统动量守恒,以v的速度方向为正方向,
由动量守恒定律得:mv-2mv′=0,解得:v′=$\frac{1}{2}$v,
设两块爆竹落地用的时间为t,则有:h=$\frac{1}{2}$gt2,
落地点,两者间的距离为:△x=(v+v′)t,
解得:△x=$\frac{3v}{2}$$\sqrt{\frac{2h}{g}}$.
故选:C.
点评 本题考查了求两裂片间的距离,知道爆竹爆竹过程系统动量守恒,应用动量守恒定律与平抛运动规律即可正确解题.

练习册系列答案
相关题目
18.在下列几种电流的波形图中,表示交变电流的是( )
| A. |  | B. |  | C. |  | D. |  |
19.下列说法正确的是( )
| A. | 静摩擦力对物体一定做正功 | |
| B. | 滑动摩擦力对物体一定做正功 | |
| C. | 若物体下落时,重力一定做正功 | |
| D. | 若作用力做正功,则反作用力一定做负功 |
16. 如图为两个单摆,摆球质量相等,悬线甲短,乙长,悬点O1、O2等高,将悬线拉至水平然后由静止释放,以悬点所在平面为参考平面,则两球经过最低点时( )
如图为两个单摆,摆球质量相等,悬线甲短,乙长,悬点O1、O2等高,将悬线拉至水平然后由静止释放,以悬点所在平面为参考平面,则两球经过最低点时( )
 如图为两个单摆,摆球质量相等,悬线甲短,乙长,悬点O1、O2等高,将悬线拉至水平然后由静止释放,以悬点所在平面为参考平面,则两球经过最低点时( )
如图为两个单摆,摆球质量相等,悬线甲短,乙长,悬点O1、O2等高,将悬线拉至水平然后由静止释放,以悬点所在平面为参考平面,则两球经过最低点时( )| A. | 甲球的动能大于乙球的动能 | |
| B. | 甲球的重力势能小于乙球的重力势能 | |
| C. | 甲球的机械能等于乙球的机械能 | |
| D. | 甲球悬线的拉力小于乙球悬线的拉力 |
17.关于第一宇宙速度,下列说法不正确的是( )
| A. | 它是人造地球卫星绕地球运行的最小速度 | |
| B. | 它等于人造地球卫星在近地圆形轨道上的运行速度 | |
| C. | 它是能使卫星在近地轨道运动的最小发射速度 | |
| D. | 它是卫星在椭圆轨道上运动时的近地点速度 |
 如图,足够长的水平传送带始终以大小为v=3m/s的速度向左运动.传送带上有一质量为M=2kg的小木盒,它与传送带间的动摩擦因数为μ=0.3.开始时,小木盒与传送带保持相对静止.现有两个光滑的质量均为m=1kg的小球先后相隔△t=3s自传送带左端出发,以v0=15m/s的速度在传送带上向右运动.已知第1个球出发后经t0=0.5s与木盒相遇并立即进入盒中与盒保持相对静止.取g=10m/s2.求:
如图,足够长的水平传送带始终以大小为v=3m/s的速度向左运动.传送带上有一质量为M=2kg的小木盒,它与传送带间的动摩擦因数为μ=0.3.开始时,小木盒与传送带保持相对静止.现有两个光滑的质量均为m=1kg的小球先后相隔△t=3s自传送带左端出发,以v0=15m/s的速度在传送带上向右运动.已知第1个球出发后经t0=0.5s与木盒相遇并立即进入盒中与盒保持相对静止.取g=10m/s2.求: 如图所示,一列简谐横波沿+x方向传播.已知在t=0时,波传播到x轴上的B质点,在它左边的A质点位于负最大位移处;在t=0.6s时,质点A第二次出现在正的最大位移处.则这列波的周期是0.4s;波速是5m/s;B质点的振动函数表达式是y=5sin5πtcm;t=0.6s时,质点D已运动的路程10cm.
如图所示,一列简谐横波沿+x方向传播.已知在t=0时,波传播到x轴上的B质点,在它左边的A质点位于负最大位移处;在t=0.6s时,质点A第二次出现在正的最大位移处.则这列波的周期是0.4s;波速是5m/s;B质点的振动函数表达式是y=5sin5πtcm;t=0.6s时,质点D已运动的路程10cm.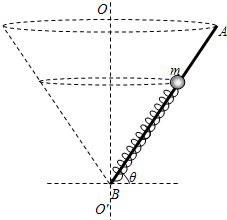 如图所示,光滑杆AB长2m,B端固定一根劲度系数为k=40N/m、原长为l0=1m的轻弹簧,质量为m=0.2kg的小球套在光滑杆上并与弹簧的上端连接.OO′为过B点的竖直轴,杆与水平面间的夹角始终为θ=53°.g取10m/s2
如图所示,光滑杆AB长2m,B端固定一根劲度系数为k=40N/m、原长为l0=1m的轻弹簧,质量为m=0.2kg的小球套在光滑杆上并与弹簧的上端连接.OO′为过B点的竖直轴,杆与水平面间的夹角始终为θ=53°.g取10m/s2 如图所示为以交流电随时间变化的图象,其中电压的正值为正弦曲线的正半周,其最大值为Um,则该交流电的电压有效值为$\frac{{\sqrt{3}}}{2}{U_m}$.
如图所示为以交流电随时间变化的图象,其中电压的正值为正弦曲线的正半周,其最大值为Um,则该交流电的电压有效值为$\frac{{\sqrt{3}}}{2}{U_m}$.