题目内容
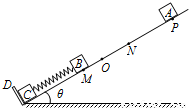 如图所示,在倾角为θ=30°的光滑斜面的底端有一个固定挡板D,小物体C靠在挡板D上,小物体B与C用轻质弹簧拴接.当弹簧处于自然长度时,B在O点;当B静止时,B在M点,OM=l.在P点还有一小物体A,使A从静止开始下滑,A、B相碰后一起压缩弹簧.A第一次脱离B后最高能上升到N点,ON=1.5l.B运动还会拉伸弹簧,使C物体刚好能脱离挡板D.A、B、C的质量都是m,重力加速度为g.求
如图所示,在倾角为θ=30°的光滑斜面的底端有一个固定挡板D,小物体C靠在挡板D上,小物体B与C用轻质弹簧拴接.当弹簧处于自然长度时,B在O点;当B静止时,B在M点,OM=l.在P点还有一小物体A,使A从静止开始下滑,A、B相碰后一起压缩弹簧.A第一次脱离B后最高能上升到N点,ON=1.5l.B运动还会拉伸弹簧,使C物体刚好能脱离挡板D.A、B、C的质量都是m,重力加速度为g.求(1)弹簧的劲度系数;
(2)弹簧第一次恢复到原长时B速度的大小;
(3)M、P之间的距离.
【答案】分析:(1)根据题意已经知道B物体平衡时弹簧的形变量,对B进行受力分析,由共点力平衡条件求出弹力,利用胡克定律得到弹簧的劲度系数;
(2)A与B分离的临界条件即弹簧恢复原长的瞬间,利用机械能守恒求出B物体的速度;
(3)综合分析A与B碰撞前、碰撞后的运动过程,找到他们遵守的物理定律即动量守恒、机械能守恒,列出方程求解.并且知道C刚刚脱离挡板的条件是弹簧的拉力与C物体沿斜面的分力相等.
解答:解:(1)B静止时,受力如图所示,
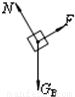
根据物体平衡条件得kl=mgsinθ
弹簧的劲度系数
(2)当弹簧第一次恢复原长时A、B恰好分离.
设此时A、B速度的大小为v3,对A物体,从A、B分离到A速度变为0的过程,
根据机械能守恒定律得
此过程中A物体上升的高度△h=1.5lsinθ
得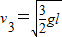
(3)设A与B相碰前速度的大小为v1,A与B相碰后速度的大小为v2,M、P之间距离为x.对A物体,从开始下滑到A、B相碰的过程,根据机械能守恒定律得
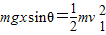
A与B发生碰撞,根据动量守恒定律得
mv1=(m+m)v2
设B静止时弹簧的弹性势能为EP,从A、B开始压缩弹簧到弹簧第一次恢复原长的过程,根据机械能守恒定律得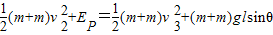
B物体的速度变为0时,C物体恰好离开挡板D,此时弹簧的伸长量也为l,弹簧的弹性势能也为EP.
对B物体和弹簧,从A、B分离到B速度变为0的过程,由机械能守恒定律得

解得
x=9l
答:(1)弹簧的劲度系数为
(2)弹簧第一次恢复到原长时B速度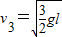
(3)M、P之间的距离x=9l
点评:本题的关键是认真分析物理过程,把复杂的物理过程分成几个小过程并且找到每个过程遵守的物理规律,
列出相应的物理方程解题.是一道全面考查动量守恒、机械能守恒的比较困难又容易出错的好题.
(2)A与B分离的临界条件即弹簧恢复原长的瞬间,利用机械能守恒求出B物体的速度;
(3)综合分析A与B碰撞前、碰撞后的运动过程,找到他们遵守的物理定律即动量守恒、机械能守恒,列出方程求解.并且知道C刚刚脱离挡板的条件是弹簧的拉力与C物体沿斜面的分力相等.
解答:解:(1)B静止时,受力如图所示,

根据物体平衡条件得kl=mgsinθ
弹簧的劲度系数

(2)当弹簧第一次恢复原长时A、B恰好分离.
设此时A、B速度的大小为v3,对A物体,从A、B分离到A速度变为0的过程,
根据机械能守恒定律得

此过程中A物体上升的高度△h=1.5lsinθ
得
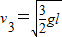
(3)设A与B相碰前速度的大小为v1,A与B相碰后速度的大小为v2,M、P之间距离为x.对A物体,从开始下滑到A、B相碰的过程,根据机械能守恒定律得
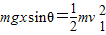
A与B发生碰撞,根据动量守恒定律得
mv1=(m+m)v2
设B静止时弹簧的弹性势能为EP,从A、B开始压缩弹簧到弹簧第一次恢复原长的过程,根据机械能守恒定律得
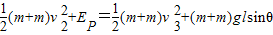
B物体的速度变为0时,C物体恰好离开挡板D,此时弹簧的伸长量也为l,弹簧的弹性势能也为EP.
对B物体和弹簧,从A、B分离到B速度变为0的过程,由机械能守恒定律得

解得
x=9l
答:(1)弹簧的劲度系数为

(2)弹簧第一次恢复到原长时B速度
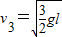
(3)M、P之间的距离x=9l
点评:本题的关键是认真分析物理过程,把复杂的物理过程分成几个小过程并且找到每个过程遵守的物理规律,
列出相应的物理方程解题.是一道全面考查动量守恒、机械能守恒的比较困难又容易出错的好题.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 如图所示,在倾角为θ=37°的斜面两端,垂直于斜面方向固定两个弹性板,两板相距d=2m,质量为m=10g,带电量为q=+1×10-7C的物体与斜面间的动摩擦因数为μ=0.2,物体从斜面中点以大小为v0=10m/s的速度沿斜面开始运动.若物体与弹性板碰撞过程中机械能不损失,电量也不变,匀强电场(方向与斜面平行)的场强E=2×106N/C,求物体在斜面上运动的总路程.(g取10m/s2 sin37°=0.6 cos37°=0.8)
如图所示,在倾角为θ=37°的斜面两端,垂直于斜面方向固定两个弹性板,两板相距d=2m,质量为m=10g,带电量为q=+1×10-7C的物体与斜面间的动摩擦因数为μ=0.2,物体从斜面中点以大小为v0=10m/s的速度沿斜面开始运动.若物体与弹性板碰撞过程中机械能不损失,电量也不变,匀强电场(方向与斜面平行)的场强E=2×106N/C,求物体在斜面上运动的总路程.(g取10m/s2 sin37°=0.6 cos37°=0.8) (2009?上海模拟)如图所示,在倾角为30°、静止的光滑斜面上,一辆加速下滑的小车上悬吊单摆的摆线总处于水平位置.已知车的质量和摆球的质量均为m,下列正确的是( )
(2009?上海模拟)如图所示,在倾角为30°、静止的光滑斜面上,一辆加速下滑的小车上悬吊单摆的摆线总处于水平位置.已知车的质量和摆球的质量均为m,下列正确的是( ) 如图所示,在倾角为θ的绝缘斜面上,有相距为L的A、B两点,分别固定着两个带电量均为Q的正点电荷.O为AB连线的中点,a、b是AB连线上两点,其中Aa=Bb=
如图所示,在倾角为θ的绝缘斜面上,有相距为L的A、B两点,分别固定着两个带电量均为Q的正点电荷.O为AB连线的中点,a、b是AB连线上两点,其中Aa=Bb= 如图所示,在倾角为θ=37°的足够长的斜面上,有质量为m1=2kg的长木板.开始时,长木板上有一质量为m2=1kg的小铁块(视为质点)以相对地面的初速度v0=2m/s 从长木板的中点沿长木板向下滑动,同时长木板在沿斜面向上的拉力作用下始终做速度为v=1m/s的匀速运动,小铁块最终与长木板一起沿斜面向上做匀速运动.已知小铁块与长木板、长木板与斜面间的动摩擦因数均为μ=0.9,重力加速度为g=10m/s2,sin37°=0.6,cos37°=0.8
如图所示,在倾角为θ=37°的足够长的斜面上,有质量为m1=2kg的长木板.开始时,长木板上有一质量为m2=1kg的小铁块(视为质点)以相对地面的初速度v0=2m/s 从长木板的中点沿长木板向下滑动,同时长木板在沿斜面向上的拉力作用下始终做速度为v=1m/s的匀速运动,小铁块最终与长木板一起沿斜面向上做匀速运动.已知小铁块与长木板、长木板与斜面间的动摩擦因数均为μ=0.9,重力加速度为g=10m/s2,sin37°=0.6,cos37°=0.8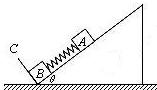 如图所示,在倾角为θ的光滑斜面上有两个用轻质弹簧相连接的物块A、B,它们的质量分别为mA、mB,弹簧的劲度系数为k,C为一固定挡板.系统处于静止状态,现开始用一恒力F沿斜面方向拉物块A使之向上运动,重力加速度为g,问:
如图所示,在倾角为θ的光滑斜面上有两个用轻质弹簧相连接的物块A、B,它们的质量分别为mA、mB,弹簧的劲度系数为k,C为一固定挡板.系统处于静止状态,现开始用一恒力F沿斜面方向拉物块A使之向上运动,重力加速度为g,问: