题目内容
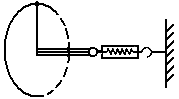
一宇航员抵达一半径为R的星球表面后,为了测定该星球的质量M,做如下的实验:取一根细线穿过光滑的细直管,细线一端拴一质量为m的砝码,另一端连接在一固定的测力计上,手握细直管抡动砝码,使它在竖直平面内做完整的圆周运动;停止抡动细直管,砝码可继续在同一竖直平面内做完整的圆周运动,如图所示.此时观察测力计得到当砝码运动到圆周的最低点和最高点两位置时测力计的读数差为ΔF.已知引力常量为G,试根据题中所提供的条件和测量结果,求出该星球的质量M.
答案:
解析:
提示:
解析:
| 解析:设星球表面重力加速度为g′,小球在圆周的最高点和最低点时,测力计读数分别为F1、F2,速度分别为v1、v2,圆周运动半径为L,则:F2-F1=ΔF
①
小球在最高点:F1+mg′=m 在最低点:F2-mg′=m 小球从最低点运动到最高点过程中机械能守恒, 由①②③④联立,得mg= 又砝码的重力为星球对其的引力,有G 联立⑤⑥得:M= 答案:M= 小结:在其他星球上,机械能守恒定律一样适用,其解题方法与地球上完全相同,只不过要结合万有引力定律联立求解.
|
提示:

练习册系列答案
相关题目
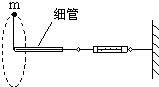 一宇航员抵达一半径为R的星球表面后,为了测定该星球的质量M,做如下的实验,取一根细线穿过光滑的细直管,细线一端栓一质量为m的砝码,另一端连在一固定的测力计上,手握细线直管抡动砝码,使它在竖直平面内做完整的圆周运动,停止抡动细直管.砝码可继续在同一竖直平面内做完整的圆周运动.如图所示,此时观察测力计得到当砝码运动到圆周的最低点和最高点两位置时,测力计的读数差为△F.已知引力常量为G,试根据题中所提供的条件和测量结果,则( )
一宇航员抵达一半径为R的星球表面后,为了测定该星球的质量M,做如下的实验,取一根细线穿过光滑的细直管,细线一端栓一质量为m的砝码,另一端连在一固定的测力计上,手握细线直管抡动砝码,使它在竖直平面内做完整的圆周运动,停止抡动细直管.砝码可继续在同一竖直平面内做完整的圆周运动.如图所示,此时观察测力计得到当砝码运动到圆周的最低点和最高点两位置时,测力计的读数差为△F.已知引力常量为G,试根据题中所提供的条件和测量结果,则( )A、该星球表面重力加速度g′=
| ||
B、该星球表面重力加速度g′=
| ||
C、该星球质量M=
| ||
D、该星球质量M=
|
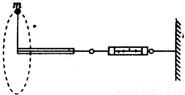
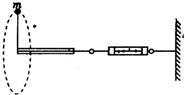 一宇航员抵达一半径为R的星球表面后,为了测定该星球的质量M,做如下实验,取一根细线穿过光滑的细直管,细线一端栓一质量为m的砝码,另一端连在一固定的测力计上,手握细直管抡动砝码,使它在竖直平面内做完整的圆周运动.停止抡动细直管,砝码可继续在同一竖直平面做完整的圆周运动.如图所示,观察测力计得到,当砝码运动到圆周的最低点时,测力计的读数为F1;当砝码运动到圆周的最高点时,测力计的读数为F2.已知引力常量为G,试根据题中提供的条件和测量结果,求:
一宇航员抵达一半径为R的星球表面后,为了测定该星球的质量M,做如下实验,取一根细线穿过光滑的细直管,细线一端栓一质量为m的砝码,另一端连在一固定的测力计上,手握细直管抡动砝码,使它在竖直平面内做完整的圆周运动.停止抡动细直管,砝码可继续在同一竖直平面做完整的圆周运动.如图所示,观察测力计得到,当砝码运动到圆周的最低点时,测力计的读数为F1;当砝码运动到圆周的最高点时,测力计的读数为F2.已知引力常量为G,试根据题中提供的条件和测量结果,求: