题目内容
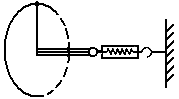
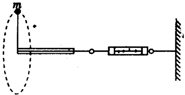
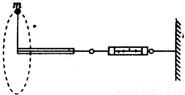
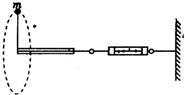 一宇航员抵达一半径为R的星球表面后,为了测定该星球的质量M,做如下实验,取一根细线穿过光滑的细直管,细线一端栓一质量为m的砝码,另一端连在一固定的测力计上,手握细直管抡动砝码,使它在竖直平面内做完整的圆周运动.停止抡动细直管,砝码可继续在同一竖直平面做完整的圆周运动.如图所示,观察测力计得到,当砝码运动到圆周的最低点时,测力计的读数为F1;当砝码运动到圆周的最高点时,测力计的读数为F2.已知引力常量为G,试根据题中提供的条件和测量结果,求:
一宇航员抵达一半径为R的星球表面后,为了测定该星球的质量M,做如下实验,取一根细线穿过光滑的细直管,细线一端栓一质量为m的砝码,另一端连在一固定的测力计上,手握细直管抡动砝码,使它在竖直平面内做完整的圆周运动.停止抡动细直管,砝码可继续在同一竖直平面做完整的圆周运动.如图所示,观察测力计得到,当砝码运动到圆周的最低点时,测力计的读数为F1;当砝码运动到圆周的最高点时,测力计的读数为F2.已知引力常量为G,试根据题中提供的条件和测量结果,求:(1)该星球表面的重力加速度;
(2)该星球的质量M;
(3)该星球的第一宇宙速度.
分析:(1)对砝码受力分析,在最高点和最低点时,由向心力的公式和整个过程的机械能守恒可以求得重力加速度的大小;
(2)求得星球表面的重力加速度的大小,再由在星球表面时,万有引力和重力近似相等,可以求得星球的质量;
(3)根据重力作为向心力,由向心力的公式可以求得星球的第一宇宙速度.
(2)求得星球表面的重力加速度的大小,再由在星球表面时,万有引力和重力近似相等,可以求得星球的质量;
(3)根据重力作为向心力,由向心力的公式可以求得星球的第一宇宙速度.
解答:解:(1)设砝码在最高点时细线的拉力为F1,速度为v1,则
F1+mg=m
①
设砝码在最低点细线的拉力为F2,速度为v2,则
F2-mg=m
②
由机械能守恒定律得
mg2r+
mV12=
mV22 ③
由①、②、③解得
g=
④
(2)在星球表面,万有引力近似等于重力
G
=m′g ⑤
由④、⑤解得
M=
(3)由mg=m
,
得 V=
=
,
答:(1)该星球表面的重力加速度是
;
(2)该星球的质量M是
;
(3)该星球的第一宇宙速度是
.
F1+mg=m
| ||
| R |
设砝码在最低点细线的拉力为F2,速度为v2,则
F2-mg=m
| ||
| R |
由机械能守恒定律得
mg2r+
| 1 |
| 2 |
| 1 |
| 2 |
由①、②、③解得
g=
| F2-F1 |
| 6m |
(2)在星球表面,万有引力近似等于重力
G
| Mm′ |
| R2 |
由④、⑤解得
M=
| (F2-F1)R2 |
| 6mG |
(3)由mg=m
| V2 |
| R |
得 V=
| gR |
|
答:(1)该星球表面的重力加速度是
| F2-F1 |
| 6m |
(2)该星球的质量M是
| (F2-F1)R2 |
| 6mG |
(3)该星球的第一宇宙速度是
|
点评:根据砝码做圆周运动时在最高点和最低点的运动规律,找出向心力的大小,可以求得重力加速度,
知道在星球表面时,万有引力和重力近似相等,而贴着星球的表面做圆周运动时,物体的重力就作为做圆周运动的向心力.
知道在星球表面时,万有引力和重力近似相等,而贴着星球的表面做圆周运动时,物体的重力就作为做圆周运动的向心力.

练习册系列答案
相关题目
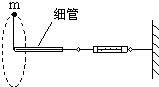 一宇航员抵达一半径为R的星球表面后,为了测定该星球的质量M,做如下的实验,取一根细线穿过光滑的细直管,细线一端栓一质量为m的砝码,另一端连在一固定的测力计上,手握细线直管抡动砝码,使它在竖直平面内做完整的圆周运动,停止抡动细直管.砝码可继续在同一竖直平面内做完整的圆周运动.如图所示,此时观察测力计得到当砝码运动到圆周的最低点和最高点两位置时,测力计的读数差为△F.已知引力常量为G,试根据题中所提供的条件和测量结果,则( )
一宇航员抵达一半径为R的星球表面后,为了测定该星球的质量M,做如下的实验,取一根细线穿过光滑的细直管,细线一端栓一质量为m的砝码,另一端连在一固定的测力计上,手握细线直管抡动砝码,使它在竖直平面内做完整的圆周运动,停止抡动细直管.砝码可继续在同一竖直平面内做完整的圆周运动.如图所示,此时观察测力计得到当砝码运动到圆周的最低点和最高点两位置时,测力计的读数差为△F.已知引力常量为G,试根据题中所提供的条件和测量结果,则( )A、该星球表面重力加速度g′=
| ||
B、该星球表面重力加速度g′=
| ||
C、该星球质量M=
| ||
D、该星球质量M=
|