题目内容
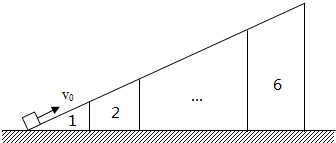
如图所示,质量为M倾角为α的斜面体(斜面光滑且足够长)放在粗糙的水平地面上,底部与地面的动摩擦因数为μ,斜面顶端与劲度系数为k、自然长度为l的轻质弹簧相连,弹簧的另一端连接着质量为m的物块.压缩弹簧使其长度为 l时将物块由静止开始释放,且物块在以后的运动中,斜面体始终处于静止状态.重力加速度为g.
l时将物块由静止开始释放,且物块在以后的运动中,斜面体始终处于静止状态.重力加速度为g.(1)求物块处于平衡位置时弹簧的长度;
(2)选物块的平衡位置为坐标原点,沿斜面向下为正方向建立坐标轴,用x表示物块相对于平衡位置的位移,证明物块做简谐运动;
(3)求弹簧的最大伸长量;
(4)为使斜面始终处于静止状态,动摩擦因数μ应满足什么条件(假设滑动摩擦力等于最大静摩擦力)?

【答案】分析:(1)物体平衡时,受重力、支持力和弹簧的弹力,三力平衡,根据平衡条件并结合正交分解法和胡克定律列式求解;
(2)简谐运动的回复力满足F=-kx形式;
(3)简谐运动具有对称性,先求解出振幅,然后确定最大伸长量;
(4)当滑块处于任意位移x处时,能保持静止即可,对斜面体受力分析后根据平衡条件列式求解,然后将最大位移打入即可.
解答:解:(1)物体平衡时,受重力、支持力和弹簧的弹力,根据平衡条件,有:
mgsinα=k?△x
解得:
故弹簧的长度为 ;
;
(2)物体到达平衡位置下方x位置时,弹力为:k(x+△x)=k(x+ );
);
故合力为:F=mgsinα-k(x+ )=-kx;
)=-kx;
故物体做简谐运动;
(3)简谐运动具有对称性,压缩弹簧使其长度为 l时将物块由静止开始释放,故其振幅为:
l时将物块由静止开始释放,故其振幅为:
A= ;
;
故其最大伸长量为:A+△x= ;
;
(4)设物块位移x为正,斜面体受重力、支持力、压力、滑动摩擦力、静摩擦力,如图

根据平衡条件,有:
水平方向:f+FN1sinα-Fcosα=0
竖直方向:FN2-Mg-FN1cosα-Fsinα=0
又有:F=k(x+△x),FN1=mgcosα
联立可得:f=kxcosα,FN2=Mg+mg+kxsinα
为使斜面体保持静止,结合牛顿第三定律,应该有|f|≤μFN2,所以

当x=-A时,上式右端达到最大值,于是有:

答:(1)物块处于平衡位置时弹簧的长度为 ;
;
(2)证明如上;
(3)弹簧的最大伸长量为 ;
;
(4)为使斜面始终处于静止状态,动摩擦因数μ应满足的条件为: .
.
点评:本题关键是先对滑块受力分析,然后根据牛顿第二定律列式分析;最后对斜面体受力分析,确定动摩擦因素的最小值,难题.
(2)简谐运动的回复力满足F=-kx形式;
(3)简谐运动具有对称性,先求解出振幅,然后确定最大伸长量;
(4)当滑块处于任意位移x处时,能保持静止即可,对斜面体受力分析后根据平衡条件列式求解,然后将最大位移打入即可.
解答:解:(1)物体平衡时,受重力、支持力和弹簧的弹力,根据平衡条件,有:
mgsinα=k?△x
解得:

故弹簧的长度为
 ;
;(2)物体到达平衡位置下方x位置时,弹力为:k(x+△x)=k(x+
 );
);故合力为:F=mgsinα-k(x+
 )=-kx;
)=-kx;故物体做简谐运动;
(3)简谐运动具有对称性,压缩弹簧使其长度为
 l时将物块由静止开始释放,故其振幅为:
l时将物块由静止开始释放,故其振幅为:A=
 ;
;故其最大伸长量为:A+△x=
 ;
;(4)设物块位移x为正,斜面体受重力、支持力、压力、滑动摩擦力、静摩擦力,如图

根据平衡条件,有:
水平方向:f+FN1sinα-Fcosα=0
竖直方向:FN2-Mg-FN1cosα-Fsinα=0
又有:F=k(x+△x),FN1=mgcosα
联立可得:f=kxcosα,FN2=Mg+mg+kxsinα
为使斜面体保持静止,结合牛顿第三定律,应该有|f|≤μFN2,所以

当x=-A时,上式右端达到最大值,于是有:

答:(1)物块处于平衡位置时弹簧的长度为
 ;
;(2)证明如上;
(3)弹簧的最大伸长量为
 ;
;(4)为使斜面始终处于静止状态,动摩擦因数μ应满足的条件为:
 .
.点评:本题关键是先对滑块受力分析,然后根据牛顿第二定律列式分析;最后对斜面体受力分析,确定动摩擦因素的最小值,难题.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
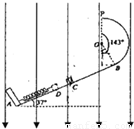
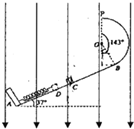 如图所示,AB为倾龟θ=37°的绝缘直轨道,轨道的AC部分光滑,CB部分粗糙.BP为半径R=1.0m的绝缘竖直光滑圆弧形轨道,O为圆心,圆心角∠BOP=143°、两轨道相切于B点,P、O两点在同一竖直线上.轻弹簧下端固定在A点上端自由伸展到C点,整个装置处在竖直向下的足够大的匀强电场中,场强E=1.0×106N/C.现有一质量m=2.0kg、带负电且电量大小恒为q=1.0×10-5C的物块(视为质点),靠在弹簧上端(不拴接),现用外力推动物块,使弹簧缓慢压缩到D点,然后迅速撤去外力,物块被反弹到C点时的速度VC=10m/So物块与轨道CB间的动摩擦因素μ=0.50,C、D间的距离L=1.Om5物块第一次经过B点后恰能到P点.(sin37°=0.6,cos37°=0.8,g 取 10m/s2)
如图所示,AB为倾龟θ=37°的绝缘直轨道,轨道的AC部分光滑,CB部分粗糙.BP为半径R=1.0m的绝缘竖直光滑圆弧形轨道,O为圆心,圆心角∠BOP=143°、两轨道相切于B点,P、O两点在同一竖直线上.轻弹簧下端固定在A点上端自由伸展到C点,整个装置处在竖直向下的足够大的匀强电场中,场强E=1.0×106N/C.现有一质量m=2.0kg、带负电且电量大小恒为q=1.0×10-5C的物块(视为质点),靠在弹簧上端(不拴接),现用外力推动物块,使弹簧缓慢压缩到D点,然后迅速撤去外力,物块被反弹到C点时的速度VC=10m/So物块与轨道CB间的动摩擦因素μ=0.50,C、D间的距离L=1.Om5物块第一次经过B点后恰能到P点.(sin37°=0.6,cos37°=0.8,g 取 10m/s2)  如图所示,粗糙斜面与光滑水平面通过半径可忽略的光滑小圆弧平滑连接,斜面倾a=37°,A、B、C是三个小滑块(可看做质点),A、B的质量均为m=1kg,B的左端附有胶泥(质量不计),C的质量均为M=2kg,D为两端分别连接B和C的轻质弹簧.
如图所示,粗糙斜面与光滑水平面通过半径可忽略的光滑小圆弧平滑连接,斜面倾a=37°,A、B、C是三个小滑块(可看做质点),A、B的质量均为m=1kg,B的左端附有胶泥(质量不计),C的质量均为M=2kg,D为两端分别连接B和C的轻质弹簧.