题目内容
4. (1)在做“用单摆测定重力加速度”的实验时,某同学尝试用DIS传感器测量周期.如图用一个磁性小球代替原先的摆球,在单摆下方放置一个磁传感器,其轴线恰好位于单摆悬挂点正下方.图中磁传感器的引出端A应接到数据采集器.使单摆做小角度摆动,当磁感应强度测量值最大时,磁性小球位于最低点.若测得连续N个磁感应强度最大值之间的时间间隔为t,则单摆周期的测量值为$\frac{2t}{N-1}$(地磁场和磁传感器的影响可忽略).
(1)在做“用单摆测定重力加速度”的实验时,某同学尝试用DIS传感器测量周期.如图用一个磁性小球代替原先的摆球,在单摆下方放置一个磁传感器,其轴线恰好位于单摆悬挂点正下方.图中磁传感器的引出端A应接到数据采集器.使单摆做小角度摆动,当磁感应强度测量值最大时,磁性小球位于最低点.若测得连续N个磁感应强度最大值之间的时间间隔为t,则单摆周期的测量值为$\frac{2t}{N-1}$(地磁场和磁传感器的影响可忽略).(2)实验中,测得重力加速度的值较当地重力加速度的值偏小的原因是:C
A.装好单摆,抓住摆球,用力拉紧,测出摆线的悬点到摆球球心之间的距离
B.让单摆自由下垂,测出摆线长度再加上摆球直径
C.计算摆长时测出摆线长没有加上摆球的半径
D.将实际振动次数n次误记成(n+1)次.
分析 (1)单摆完成一次周期性运动需要的时间是一个周期,根据题意求出单摆的周期.
(2)应用单摆周期公式求出重力加速度,然后分析实验误差.
解答 解:(1)单摆做小角度摆动,当磁感应强度测量值最大时,磁性小球位于最低点(或平衡位置).若测得连续N个磁感应强度最大值之间的时间间隔为t,是$\frac{N-1}{2}$个周期,则单摆的周期为:T=$\frac{t}{\frac{N-1}{2}}$=$\frac{2t}{N-1}$;
(2)由单摆周期公式:T=2π$\sqrt{\frac{L}{g}}$可知,重力加速度:g=$\frac{4{π}^{2}L}{{T}^{2}}$;
A、装好单摆,抓住摆球,用力拉紧,测出摆线的悬点到摆球球心之间的距离,所测摆长L偏大,由g=$\frac{4{π}^{2}L}{{T}^{2}}$可知,所测重力加速度偏大,故A错误;
B、让单摆自由下垂,测出摆线长度再加上摆球直径,所测摆长L偏大,由g=$\frac{4{π}^{2}L}{{T}^{2}}$可知,所测重力加速度偏大,故B错误;
C、计算摆长时测出摆线长没有加上摆球的半径所测摆长L偏小,由g=$\frac{4{π}^{2}L}{{T}^{2}}$可知,所测重力加速度偏小,故C正确;
D、将实际振动次数n次误记成(n+1)次,所测周期T偏小,由g=$\frac{4{π}^{2}L}{{T}^{2}}$可知,所测重力加速度偏大,故D错误;故选C.
故答案为:(1)$\frac{2t}{N-1}$;(2)C.
点评 本题考查了求单摆的周期、试验误差分析,知道周期的定义、应用单摆周期公式可以解题,平时要注意基础知识的学习与掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15. 如图所示,一列简谐横波在同种均匀介质中以速度v=1m/s沿x轴正方向传播,a、b、c、d是x轴上的四个质点,相邻两点间距离依次为1m、2m和4m.t=0时波恰传到质点a处,且质点a从平衡位置开始竖直向上运动t=11s时质点a第三次到达最低点.下列判断中正确的是( )
如图所示,一列简谐横波在同种均匀介质中以速度v=1m/s沿x轴正方向传播,a、b、c、d是x轴上的四个质点,相邻两点间距离依次为1m、2m和4m.t=0时波恰传到质点a处,且质点a从平衡位置开始竖直向上运动t=11s时质点a第三次到达最低点.下列判断中正确的是( )
 如图所示,一列简谐横波在同种均匀介质中以速度v=1m/s沿x轴正方向传播,a、b、c、d是x轴上的四个质点,相邻两点间距离依次为1m、2m和4m.t=0时波恰传到质点a处,且质点a从平衡位置开始竖直向上运动t=11s时质点a第三次到达最低点.下列判断中正确的是( )
如图所示,一列简谐横波在同种均匀介质中以速度v=1m/s沿x轴正方向传播,a、b、c、d是x轴上的四个质点,相邻两点间距离依次为1m、2m和4m.t=0时波恰传到质点a处,且质点a从平衡位置开始竖直向上运动t=11s时质点a第三次到达最低点.下列判断中正确的是( )| A. | 在t=8s时波恰好传到质点d处 | |
| B. | 在t=5s时质点c恰好到达最高点 | |
| C. | 在4s<t<6s时间内质点c正向上运动 | |
| D. | 在质点d向上运动时质点b一定向下运动 |
12. 如图所示,固定的竖直光滑U型金属导轨,间距为L,上端接有阻值为R的电阻,处在方向水平且垂直于导轨平面、磁感应强度为B的匀强磁场中,质量为m、电阻为r的导体棒与劲度系数为k的固定轻弹簧相连放在导轨上,导轨的电阻忽略不计.初始时刻,弹簧处于伸长状态,其伸长量为x1=$\frac{mg}{k}$,此时导体棒具有竖直向上的初速度v0.在沿导轨往复运动的过程中,导体棒始终与导轨垂直并保持良好接触.则下列说法正确的是( )
如图所示,固定的竖直光滑U型金属导轨,间距为L,上端接有阻值为R的电阻,处在方向水平且垂直于导轨平面、磁感应强度为B的匀强磁场中,质量为m、电阻为r的导体棒与劲度系数为k的固定轻弹簧相连放在导轨上,导轨的电阻忽略不计.初始时刻,弹簧处于伸长状态,其伸长量为x1=$\frac{mg}{k}$,此时导体棒具有竖直向上的初速度v0.在沿导轨往复运动的过程中,导体棒始终与导轨垂直并保持良好接触.则下列说法正确的是( )
 如图所示,固定的竖直光滑U型金属导轨,间距为L,上端接有阻值为R的电阻,处在方向水平且垂直于导轨平面、磁感应强度为B的匀强磁场中,质量为m、电阻为r的导体棒与劲度系数为k的固定轻弹簧相连放在导轨上,导轨的电阻忽略不计.初始时刻,弹簧处于伸长状态,其伸长量为x1=$\frac{mg}{k}$,此时导体棒具有竖直向上的初速度v0.在沿导轨往复运动的过程中,导体棒始终与导轨垂直并保持良好接触.则下列说法正确的是( )
如图所示,固定的竖直光滑U型金属导轨,间距为L,上端接有阻值为R的电阻,处在方向水平且垂直于导轨平面、磁感应强度为B的匀强磁场中,质量为m、电阻为r的导体棒与劲度系数为k的固定轻弹簧相连放在导轨上,导轨的电阻忽略不计.初始时刻,弹簧处于伸长状态,其伸长量为x1=$\frac{mg}{k}$,此时导体棒具有竖直向上的初速度v0.在沿导轨往复运动的过程中,导体棒始终与导轨垂直并保持良好接触.则下列说法正确的是( )| A. | 初始时刻导体棒受到的安培力大小F=$\frac{{B}^{2}{L}^{2}{v}_{0}}{R}$ | |
| B. | 初始时刻导体棒加速度的大小a=2g+$\frac{{B}^{2}{L}^{2}{v}_{0}}{m(R+r)}$ | |
| C. | 导体棒往复运动,最终将静止时弹簧处于压缩状态 | |
| D. | 导体棒开始运动直到最终静止的过程中,电阻R上产生的焦耳热Q=$\frac{1}{2}$mv02+$\frac{2{m}^{2}{g}^{2}}{k}$ |
19.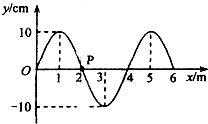 一列简谐横波在t=0时的波形图如图所示.介质中x=2m处的质点P沿y轴方向做简谐运动的表达式为y=-10sin(5πt)cm.关于这列简谐波,下列说法正确的是( )
一列简谐横波在t=0时的波形图如图所示.介质中x=2m处的质点P沿y轴方向做简谐运动的表达式为y=-10sin(5πt)cm.关于这列简谐波,下列说法正确的是( )
 一列简谐横波在t=0时的波形图如图所示.介质中x=2m处的质点P沿y轴方向做简谐运动的表达式为y=-10sin(5πt)cm.关于这列简谐波,下列说法正确的是( )
一列简谐横波在t=0时的波形图如图所示.介质中x=2m处的质点P沿y轴方向做简谐运动的表达式为y=-10sin(5πt)cm.关于这列简谐波,下列说法正确的是( )| A. | 传播方向沿x轴正向 | B. | 周期为2.5s | ||
| C. | 传播速度为10m/s | D. | 经一个周期,质点P通过的路程为4m |
13. 中国北斗卫星导航系统是我国自行研制的全球卫星定位与通信系统.是继美国全球定位系统和俄罗斯全球卫星导航系统之后第三个成熟的卫星导航系统.系统由空间端、地面端和用户端组成,其中空间端包括5颗地球同步卫星和30非地球同步卫星,如图所示.下列说法中正确的是( )
中国北斗卫星导航系统是我国自行研制的全球卫星定位与通信系统.是继美国全球定位系统和俄罗斯全球卫星导航系统之后第三个成熟的卫星导航系统.系统由空间端、地面端和用户端组成,其中空间端包括5颗地球同步卫星和30非地球同步卫星,如图所示.下列说法中正确的是( )
 中国北斗卫星导航系统是我国自行研制的全球卫星定位与通信系统.是继美国全球定位系统和俄罗斯全球卫星导航系统之后第三个成熟的卫星导航系统.系统由空间端、地面端和用户端组成,其中空间端包括5颗地球同步卫星和30非地球同步卫星,如图所示.下列说法中正确的是( )
中国北斗卫星导航系统是我国自行研制的全球卫星定位与通信系统.是继美国全球定位系统和俄罗斯全球卫星导航系统之后第三个成熟的卫星导航系统.系统由空间端、地面端和用户端组成,其中空间端包括5颗地球同步卫星和30非地球同步卫星,如图所示.下列说法中正确的是( )| A. | 这5颗地球同步卫星离地面的高度不一定相同 | |
| B. | 这5颗地球同步卫星的运行周期都与地球自转周期相等 | |
| C. | 这5颗地球同步卫星的加速度不一定相同 | |
| D. | 为避免卫星相撞,不同国家发射的地球同步卫星必须运行在不同的轨道上 |
 如图1所示,两根足够长平行金属导轨MN、PQ相距为L,导轨平面与水平面夹角为α,金属棒ab垂直于MN、PQ放置在导轨上,且始终与导轨接触良好,金属棒的质量为m,电阻与R1相等.导轨处于匀强磁场中,磁场的方向垂直于导轨平面斜向上,磁感应强度大小为B.金属导轨的上端与开关S、定值电阻R1和电阻箱R2相连.不计一切摩擦,不计导轨的电阻,重力加速度为g.现在闭合开关S,将金属棒由静止释放.求:
如图1所示,两根足够长平行金属导轨MN、PQ相距为L,导轨平面与水平面夹角为α,金属棒ab垂直于MN、PQ放置在导轨上,且始终与导轨接触良好,金属棒的质量为m,电阻与R1相等.导轨处于匀强磁场中,磁场的方向垂直于导轨平面斜向上,磁感应强度大小为B.金属导轨的上端与开关S、定值电阻R1和电阻箱R2相连.不计一切摩擦,不计导轨的电阻,重力加速度为g.现在闭合开关S,将金属棒由静止释放.求: 改进后的“研究有固定转动轴物体平衡条件”的实验装置如图所示,力传感器、定滑轮固定在横杆上,替代原装置中的弹簧秤.已知力矩盘上各同心圆的间距为5cm.
改进后的“研究有固定转动轴物体平衡条件”的实验装置如图所示,力传感器、定滑轮固定在横杆上,替代原装置中的弹簧秤.已知力矩盘上各同心圆的间距为5cm.