题目内容
如图所示，压路机大轮的半径R是小轮半径r的2倍，压路机匀速行驶时，大轮边缘上A点的向心加速度是12 cm/s2，那么小轮边缘上B点的向心加速度是多少？大轮上距轴心的距离为R/3的C点的向心加速度大小是多少？
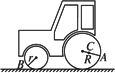
答案：
解析：
解析：
|
答案：ab＝24 cm/s2；ac＝4 cm/s2 解析：压路机的前后轮的半径虽然不同，但它们在相同时间内轮沿上的点转过的弧长相等，因此，A、B两点的线速度相同；而A、C共轴，角速度相同．A、B两点的线速度相同，由a＝ |
得
，所以aB＝2aA＝24 cm/s2．A、C两点角速度相同，由a＝ω2R得
＝3，aC＝
cm/s2．
练习册系列答案
相关题目
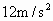，那么小轮边缘上的B点向心加速度是__________
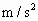，大轮上距轴心的距离为？的C点的向心加速度是__________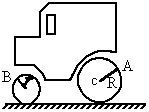
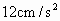，那么小轮边缘上的B点向心加速度是多少？大轮上距轴心的距离为
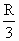的C的向心加速度是多大？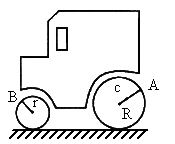
，那么小轮边缘上B点的向心加速度大小是多少？大轮上距轴心的距离为
的C点的向心加速度大小是多少？
