Question

一带电质点质量为m、电量为q，以平行于Ox轴的速度v从y轴上的a点射入图中第一象限所示的区域，为了使该质点能从x轴上的b点以垂直于Ox轴的速度v射出，可在适当的地方加一个垂直于xy平面、磁感应强度为B的匀强磁场．若此磁场仅分布在一个圆形区域内，试求这圆形磁场区域的最小半径．重力忽略不计．

Answer 1

答案：
解析：

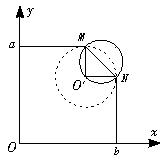
解题方法：程序法． 解析：（1）画轨迹，找圆心O′． 题设质点从a点射入第一象限，从b点射出，两方向垂直，因此它在磁场中的径迹应是圆的圆周，并分别与va、vb方向相切． 过a点作平行于x轴的直线，过b点作平行于y轴的直线，则与这两直线距离均为R的O′就是圆周的圆心．质点在磁场区域中的轨道就是以O′为圆心，R为半径的圆（图中的虚线圆）上的弧MN，M点和N点应在所求圆形磁场区域的边界上． (2)确定半径R 由于质点的质量、带电量、运动速度的大小以及所加磁场的磁感应强度均为定值，因此，质点在垂直于磁场的xOy平面内做匀速圆周运动的半径R亦为定值．即由qvB＝m得R＝mv/(qB)① (3)求圆形磁场区域的最小半径r 以M、N两点连线为弦可以作许多圆，其中在通过M、N两点的不同圆周中，最小的一个是以线段为直径的圆周，所以本题中所求的圆形磁场区域的最小半径为 r＝＝＝＝·② 所求磁场区域如图中的实线所示．

提示：

点评：（1）解本题首先要根据题中条件画出轨迹，找到圆心，然后运用F向＝F洛确定轨迹半径R．在解本题中，运用了一些关于圆的几何知识，体现了高考考查运用数学工具分析解决物理问题的能力，求解本题的难点是要弄清圆轨道半径R与圆形匀强磁场区域半径r的区别和联系，而不少考生将两者混在了一起，从而求解错误． （2）本题的粒子轨迹为圆弧，磁场也在一个圆形区域里，此类问题可称之为“圆中圆”问题，解此类问题应注意到:①粒子入场点和出场点既是粒子轨道圆弧上的点，也是磁场圆周上的点，具有双重身份，是联系两圆的桥梁，是解答此类问题的关键之一；②粒子速度偏转角等于轨道圆心角．