题目内容
如图所示，在竖直方向上A、B两物体通过劲度系数为k的轻质弹簧相连，A放在水平地面上；B、C两物体通过细绳绕过轻质定滑轮相连，C放在固定的光滑斜面上．用手拿住C，使细线刚刚拉直但无拉力作用，并保证ab段的细线竖直、cd段的细线与斜面平行．已知A、B的质量均为m，C的质量为4 m，重力加速度为g，细线与滑轮之间的摩擦不计，开始时整个系统处于静止状态．释放C后它沿斜面下滑，A刚离开地面时，B获得最大速度，求：
(1)斜面倾角α．
(2)B的最大速度VBm．
答案：
解析：
解析：
|
解：(1)设当物体A刚刚离开地面时，弹簧的伸长量为为xA，由： kxA＝mg(1分) 此时以B为研究对象，物体B受到重力mg、弹簧的弹力kxA、细线的拉力T三个力的作用．设物体B的加速度为a，根据牛顿第二定律， 对B有：T－mg－kxA＝ma(1分) 对C有：4mgsinα－T＝4ma(1分) 由以上两式得：4mgsinα－mg－kxA＝5ma(1分) 当B获得最大速度时，有：a＝0 解得：sinα＝1/2 所以：α＝30°(1分) (2)开始时弹簧压缩的长度为：xB＝mg/k(1分) 当物体A刚离开地面时，物体B上升的距离以及物体C沿斜面下滑的距离为：h＝xA＋xB(1分) 由于xA＝xB，弹簧处于压缩状态和伸长状态时的弹性势能相等，弹簧弹力做功为零．且物体A刚刚离开地面时，B、C两物体的速度相等，设为vBm，由动能定理： 解得： |
(2分)
(1分)
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
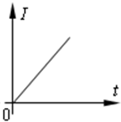
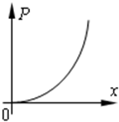
如图所示，在竖直方向的磁感应强度为B的匀强磁场中，金属框架ABCD（框架电阻忽略不计）固定在水平面内，AB与CD平行且足够长，BC与CD夹角θ（θ＜90°），光滑均匀导体棒EF（垂直于CD）在外力作用下以垂直于自身的速度v向右匀速运动，导体棒在滑动过程中始终保持与框架良好接触，经过C点瞬间作为计时起点，下列关于电路中电流大小I与时间t、消耗的电功率P与导体棒水平移动的距离x变化规律的图象中正确的是（ ）
如图所示，在竖直方向的磁感应强度为B的匀强磁场中，金属框架ABCD（框架电阻忽略不计）固定在水平面内，AB与CD平行且足够长，BC与CD夹角θ（θ＜90°），光滑均匀导体棒EF（垂直于CD）紧贴框架，在外力作用下以垂直于自身的速度v向右匀速运动，经过C点作为计时起 点，下列关于电路中电流大小I与时间t、消耗的电功率P与导体棒水平移动的距离x变化规律的图象中正确的是（ ）
如图所示是在竖直方向上振动并沿水平方向传播的简谐波，实线是t=0s时刻的波形图，虚线是t=0.2s时刻的波形图．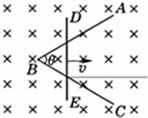
如图所示，在竖直方向的磁感应强度为B的匀强磁场中，金属框架ABC固定在水平面内，AB与BC间夹角为θ，光滑导体棒DE在框架上从B点开始在外力作用下以速度v向右匀速运动，导体棒与框架足够长且构成等腰三角形电路．若框架与导体棒单位长度的电阻均为R，导体棒在滑动过程中始终保持与导轨良好接触，下列关于电路中电流大小I与时间t、消耗的电功率P与水平移动的距离x变化规律的图象中正确的是（ ）
