题目内容
质量为m的带电小球,从固定在地面上的半径为R的光滑半圆轨道顶处由静止开始沿逆时针方向滑下.(1)若整个装置处于磁感强度为B、方向垂直轨道平面向里的匀强磁场中,如图所示,且小球始终未离开轨道表面,小球应带何种电荷?电量至少多少?
(2)如果去掉磁场,而其它条件不变,小球会在什么地方离开轨道?

【答案】分析:(1)分析小球的受力:重力、支持力,洛仑兹力,只有重力做功,其机械能守恒.小球在轨道最低点最容易离开轨道表面,由题意小球始终未离开轨道表面,在最低点由洛伦兹力的支持力的合力提供向心力,当支持力N=0时,洛伦兹力最小,电量最小.由机械能守恒和牛顿第二定律求解.
(2)如果去掉磁场,小球在到达最低点前离开轨道,刚离开时轨道的支持力为零,由重力沿半径方向的分力提供向心力,根据牛顿第二定律和机械能守恒结合求小球与轨道球心连线和竖直方向的夹角.
解答: 解:(1)小球沿半球表面滑下至最低点的过程受重力、支持力,洛仑兹力这三个力的作用,但只有重力做功,机械能守恒,则有
解:(1)小球沿半球表面滑下至最低点的过程受重力、支持力,洛仑兹力这三个力的作用,但只有重力做功,机械能守恒,则有
mgR= mv2
mv2
设小球下滑至最低点时的速度为v,则:v= ①
①
在最低点有:QvB-N=m
由①知小球在最低点的速度v是一定的,要使Q最小,则必须N=0,设此时的油滴电量为Q,即 QvB=m ②
②
联解①、②得带电量至少为 Q= ,
,
由左手定则判断知:小球带正电.
(2)设小球在与过圆心的竖直半径成θ角处离开球面,此刻速度为v1
则在此处有:mgcosθ-N=m ①
①
小球在离开球面处有 N=0 ②
又据机械能守恒定律:mgR(1-cosθ)= ③
③
联解①②③得:cosθ=
即:θ=arccos
当小球滑至与球心连线与竖直方向成cos-1 角的位置时离开轨道.
角的位置时离开轨道.
答:
(1)小球带正电,电量至少 ,
,
(2)如果去掉磁场,而其它条件不变,当小球滑至与球心连线与竖直方向成cos-1 角的位置时离开轨道.
角的位置时离开轨道.
点评:本题的解题关键是确定临界条件:当小球刚离开轨道时,支持力为零,再根据牛顿第二定律、机械能守恒和向心力进行求解.
(2)如果去掉磁场,小球在到达最低点前离开轨道,刚离开时轨道的支持力为零,由重力沿半径方向的分力提供向心力,根据牛顿第二定律和机械能守恒结合求小球与轨道球心连线和竖直方向的夹角.
解答:
 解:(1)小球沿半球表面滑下至最低点的过程受重力、支持力,洛仑兹力这三个力的作用,但只有重力做功,机械能守恒,则有
解:(1)小球沿半球表面滑下至最低点的过程受重力、支持力,洛仑兹力这三个力的作用,但只有重力做功,机械能守恒,则有 mgR=
 mv2
mv2设小球下滑至最低点时的速度为v,则:v=
 ①
①在最低点有:QvB-N=m

由①知小球在最低点的速度v是一定的,要使Q最小,则必须N=0,设此时的油滴电量为Q,即 QvB=m
 ②
②联解①、②得带电量至少为 Q=
 ,
,由左手定则判断知:小球带正电.
(2)设小球在与过圆心的竖直半径成θ角处离开球面,此刻速度为v1
则在此处有:mgcosθ-N=m
 ①
①小球在离开球面处有 N=0 ②
又据机械能守恒定律:mgR(1-cosθ)=
 ③
③联解①②③得:cosθ=

即:θ=arccos

当小球滑至与球心连线与竖直方向成cos-1
 角的位置时离开轨道.
角的位置时离开轨道.答:
(1)小球带正电,电量至少
 ,
,(2)如果去掉磁场,而其它条件不变,当小球滑至与球心连线与竖直方向成cos-1
 角的位置时离开轨道.
角的位置时离开轨道.点评:本题的解题关键是确定临界条件:当小球刚离开轨道时,支持力为零,再根据牛顿第二定律、机械能守恒和向心力进行求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 在空间中水平面MN的下方存在竖直向下的匀强电场,质量为m的带电小球由MN上方的A点以一定初速度水平抛出,从B点进入电场,到达C点时速度方向恰好水平,A、B、C三点在同一直线上,且AB=2BC,如图所示.由此可见( )
在空间中水平面MN的下方存在竖直向下的匀强电场,质量为m的带电小球由MN上方的A点以一定初速度水平抛出,从B点进入电场,到达C点时速度方向恰好水平,A、B、C三点在同一直线上,且AB=2BC,如图所示.由此可见( )| A、电场力为mg | B、小球带正电 | C、小球从A到B与从B到C的运动时间相等 | D、小球从A到B与从B到C的速度变化量大小相等 |
 半径为R的光滑绝缘半球槽处在水平向右的匀强电场中,一质量为m的带电小球从槽的右端A处(与球心等高)无初速度沿轨道滑下,滑到最低点B时,球对轨道的压力为2mg.求:
半径为R的光滑绝缘半球槽处在水平向右的匀强电场中,一质量为m的带电小球从槽的右端A处(与球心等高)无初速度沿轨道滑下,滑到最低点B时,球对轨道的压力为2mg.求: (2009?长宁区二模)长为l的绝缘细线下端系一质量为m的带电小球a,细线悬挂点位于x轴正上方高为h(h>l)处,小球a同时受到水平绝缘细线的拉力而静止,如图所示.现保持悬线与竖直方向的夹角为θ,在x轴上放置另一带电小球b,让其从o点沿x轴正向移动到某一位置时,使水平绝缘细线的拉力恰减小为零,悬线的拉力恰为mgcosθ,在此过程中悬线中拉力的变化情况是
(2009?长宁区二模)长为l的绝缘细线下端系一质量为m的带电小球a,细线悬挂点位于x轴正上方高为h(h>l)处,小球a同时受到水平绝缘细线的拉力而静止,如图所示.现保持悬线与竖直方向的夹角为θ,在x轴上放置另一带电小球b,让其从o点沿x轴正向移动到某一位置时,使水平绝缘细线的拉力恰减小为零,悬线的拉力恰为mgcosθ,在此过程中悬线中拉力的变化情况是 如图所示,一长为L的丝线上端固定,下端拴一质量为m的带电小球,将它置于一水平向右的匀强电场E中,当细线偏角为θ时,小球处于平衡状态.试问:
如图所示,一长为L的丝线上端固定,下端拴一质量为m的带电小球,将它置于一水平向右的匀强电场E中,当细线偏角为θ时,小球处于平衡状态.试问: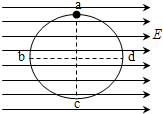 一半径为R的光滑圆环竖直放在水平向右的场强为E的匀强电场中,如图所示,环上a、c是竖直直径的两端,b、d是水平直径的两端,质量为m的带电小球套在圆环上,并可沿环无摩擦滑动,已知小球自a点由静止释放,沿abc运动到d点时速度恰好为零,由此可知( )
一半径为R的光滑圆环竖直放在水平向右的场强为E的匀强电场中,如图所示,环上a、c是竖直直径的两端,b、d是水平直径的两端,质量为m的带电小球套在圆环上,并可沿环无摩擦滑动,已知小球自a点由静止释放,沿abc运动到d点时速度恰好为零,由此可知( )