题目内容
 半径为R的光滑绝缘半球槽处在水平向右的匀强电场中,一质量为m的带电小球从槽的右端A处(与球心等高)无初速度沿轨道滑下,滑到最低点B时,球对轨道的压力为2mg.求:
半径为R的光滑绝缘半球槽处在水平向右的匀强电场中,一质量为m的带电小球从槽的右端A处(与球心等高)无初速度沿轨道滑下,滑到最低点B时,球对轨道的压力为2mg.求:(1)小球从A到B的过程中电场力做的功及电场力的大小;
(2)带电小球在滑动过程中的最大速度.
分析:(1)设小球运动到最底位置B时速度为v,小球从A处沿槽滑到最底位置B的过程中,根据动能定理结合向心力公式联立方程即可求解;
(2)小球在滑动过程中最大速度的条件:是小球沿轨道运动过程某位置时切向合力为零,设此时小球和圆心间的连线与竖直方向的夹角为θ,根据几何关系及动能定理即可求解.
(2)小球在滑动过程中最大速度的条件:是小球沿轨道运动过程某位置时切向合力为零,设此时小球和圆心间的连线与竖直方向的夹角为θ,根据几何关系及动能定理即可求解.
解答:解:(1)设小球运动到最低位置B时速度为v,此时N-mg=
…①
由题意,N=2mg
解得:v=
设电场力大小为F,做功为W,小球从A处沿槽滑到最底位置B的过程中,根据动能定理得:mgR+W=
mv2-0…②
由①、②两式得:W=-
mgR…③
所以此过程中电场力做负功,则电场力方向水平向右,由|W|=FR,得电场力大小为 F=|
|=
mg.
(2)小球在滑动过程中最大速度的条件:是小球沿轨道运动过程某位置时切向合力为零,设此时小球和圆心间的连线与竖直方向的夹角为θ,如图
mgsinθ=Fcosθ…③
则得:tanθ=
小球由A处到最大速度位置得过程中,由动能定理得:
mgRcosθ-
mgR(1-sinθ)=
m
-0
解得 vm=
答:(1)小球受到电场力的大小为
mg,方向水平向右;
(2)带电小球在滑动过程中的最大速度是
.
| v2 |
| R |

由题意,N=2mg
解得:v=
| gR |
设电场力大小为F,做功为W,小球从A处沿槽滑到最底位置B的过程中,根据动能定理得:mgR+W=
| 1 |
| 2 |
由①、②两式得:W=-
| 1 |
| 2 |
所以此过程中电场力做负功,则电场力方向水平向右,由|W|=FR,得电场力大小为 F=|
| W |
| R |
| 1 |
| 2 |
(2)小球在滑动过程中最大速度的条件:是小球沿轨道运动过程某位置时切向合力为零,设此时小球和圆心间的连线与竖直方向的夹角为θ,如图
mgsinθ=Fcosθ…③
则得:tanθ=
| 1 |
| 2 |
小球由A处到最大速度位置得过程中,由动能定理得:
mgRcosθ-
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 m |
解得 vm=
(
|
答:(1)小球受到电场力的大小为
| 1 |
| 2 |
(2)带电小球在滑动过程中的最大速度是
(
|
点评:本题主要考查了动能定理及向心力公式的直接应用,要注意电场力方向的判断,难度适中.

练习册系列答案
相关题目
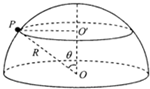 (2008?四川)如图,一半径为R的光滑绝缘半球面开口向下,固定在水平面上.整个空间存在匀强磁场,磁感应强度方向竖直向下.一电荷量为q(q>0)、质量为m的小球P在球面上做水平的匀速圆周运动,圆心为O′.球心O到该圆周上任一点的连线与竖直方向的夹角为θ(0<θ<
(2008?四川)如图,一半径为R的光滑绝缘半球面开口向下,固定在水平面上.整个空间存在匀强磁场,磁感应强度方向竖直向下.一电荷量为q(q>0)、质量为m的小球P在球面上做水平的匀速圆周运动,圆心为O′.球心O到该圆周上任一点的连线与竖直方向的夹角为θ(0<θ< 如图,一半径为R的光滑绝缘半球面开口向下,固定在水平面上。整个空间存在匀强磁场,磁感应强度方向竖直向下。一电荷量为q(q>0)、质量为m的小球P在球面上做水平的匀速圆周运动,圆心为O’。球心O到该圆周上任一点的连线与竖直方向的夹角为θ(0<θ<
如图,一半径为R的光滑绝缘半球面开口向下,固定在水平面上。整个空间存在匀强磁场,磁感应强度方向竖直向下。一电荷量为q(q>0)、质量为m的小球P在球面上做水平的匀速圆周运动,圆心为O’。球心O到该圆周上任一点的连线与竖直方向的夹角为θ(0<θ< 如图,一半径为R的光滑绝缘半球面开口向下,固定在水平面上。整个空间存在匀强磁场,磁感应强度方向竖直向下。一电荷量为q(q>0)、质量为m的小球P在球面上做水平的匀速圆周运动,圆心为O’。球心O到该圆周上任一点的连线与竖直方向的夹角为θ(0<θ<
如图,一半径为R的光滑绝缘半球面开口向下,固定在水平面上。整个空间存在匀强磁场,磁感应强度方向竖直向下。一电荷量为q(q>0)、质量为m的小球P在球面上做水平的匀速圆周运动,圆心为O’。球心O到该圆周上任一点的连线与竖直方向的夹角为θ(0<θ< (08四川卷)24.(19分)如图,一半径为R的光滑绝缘半球面开口向下,固定在水平面上。整个空间存在匀强磁场,磁感应强度方向竖直向下。一电荷量为q(q>0)、质量为m的小球P在球面上做水平的匀速圆周运动,圆心为O’。球心O到该圆周上任一点的连线与竖直方向的夹角为θ(0<θ<
(08四川卷)24.(19分)如图,一半径为R的光滑绝缘半球面开口向下,固定在水平面上。整个空间存在匀强磁场,磁感应强度方向竖直向下。一电荷量为q(q>0)、质量为m的小球P在球面上做水平的匀速圆周运动,圆心为O’。球心O到该圆周上任一点的连线与竖直方向的夹角为θ(0<θ< .为了使小球能够在该圆周上运动,求磁感应强度大小的最小值及小球P相应的速率.重力加速度为g.
.为了使小球能够在该圆周上运动,求磁感应强度大小的最小值及小球P相应的速率.重力加速度为g.