题目内容
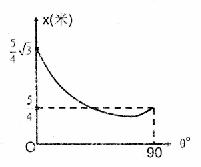
 如图所示,一物以一定初速v0沿斜面向上运动,此物在斜面上的最大位移与斜面倾角的关系由图中曲线给出.试求:
如图所示,一物以一定初速v0沿斜面向上运动,此物在斜面上的最大位移与斜面倾角的关系由图中曲线给出.试求:(1)摩擦因数μ;
(2)当θ=60°时x的值是多少.(g=10m/s2,且各种θ条件下,摩擦因数不变)
分析:(1)当倾角为90度时,物体做竖直上抛运动,当倾角为0度时,做匀减速直线运动,结合牛顿第二定律和运动学公式求出物体与斜面间的动摩擦因数.
(2)根据动能定理列方程求当θ=60°时x的值.
(2)根据动能定理列方程求当θ=60°时x的值.
解答:解:(1)当倾角为90度时,加速度大小为g,则
=
,
当倾角为0度时,加速度大小为a=μg,则
=
,
联立得μ=
;
(2)根据动能定理:
mV02=mgx?sin60°+μmgx?cos60°
得x=
m=1.08m
答:(1)摩擦因数μ为
;
(2)当θ=60°时x的值是1.08m.
| V02 |
| 2g |
| 5 |
| 4 |
当倾角为0度时,加速度大小为a=μg,则
| v02 |
| 2μg |
| 5 |
| 4 |
| 3 |
联立得μ=
| ||
| 3 |
(2)根据动能定理:
| 1 |
| 2 |
得x=
| 5 |
| 8 |
| 3 |
答:(1)摩擦因数μ为
| ||
| 3 |
(2)当θ=60°时x的值是1.08m.
点评:本题考查了牛顿第二定律和运动学公式的基本运用,以及动能定理的应用,知道加速度是联系力学和运动学的桥梁.

练习册系列答案
相关题目
 一物块以一定的初速度沿斜面向上滑出,利用速度传感器可以在计算机屏幕上得到其速度大小随时间的变化关系图象如图所示,则物块( )
一物块以一定的初速度沿斜面向上滑出,利用速度传感器可以在计算机屏幕上得到其速度大小随时间的变化关系图象如图所示,则物块( )| A、上滑过程的加速度大小为8m/s2 | B、下滑过程的加速度与上滑过程的加速度方向相反 | C、物块在斜面上不受摩擦力作用 | D、物块在1.5s时刻回到出发点 |
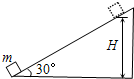 如图所示,一固定斜面倾角为30°,一质量为m的小物块自斜面底端以一定的初速度沿斜面向上做匀减速运动,加速度大小等于重力加速度的大小g.物块上升的最大高度为H,则此过程中,物块的( )
如图所示,一固定斜面倾角为30°,一质量为m的小物块自斜面底端以一定的初速度沿斜面向上做匀减速运动,加速度大小等于重力加速度的大小g.物块上升的最大高度为H,则此过程中,物块的( ) (2011?泗阳县一模) (选做题)本题包括A、B、C三小题,请选定其中两题,并在相应答题区域内作答.若三题都做,则按A、B两题评分.
(2011?泗阳县一模) (选做题)本题包括A、B、C三小题,请选定其中两题,并在相应答题区域内作答.若三题都做,则按A、B两题评分.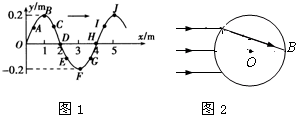 (3)图2示是一透明的圆柱体的横截面,其半径R=20cm,折射率为
(3)图2示是一透明的圆柱体的横截面,其半径R=20cm,折射率为