题目内容
在高速公路的拐弯处，通常路面都是外高内低．如图所示，在某路段汽车向左拐弯，司机左侧的路面比右侧的路面低一些．汽车的运动可看作是做半径为R的在水平面内的圆周运动．设内外路面高度差为h，路基的水平宽度为d，路面的宽度为L．已知重力加速度为g．要使车轮与路面之间的横向摩擦力（即垂直于前进方向）等于零，则汽车转弯时的车速应等于（ ）
A．
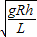
B．
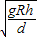
C．
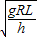
D．
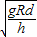
【答案】分析：要使车轮与路面之间的横向摩擦力等于零，则汽车转弯时，由路面的支持力与重力的合力提供汽车的向心力，根据牛顿第二定律，结合数学知识求解车速．
解答：解：设路面的斜角为θ，作出汽车的受力图，如图．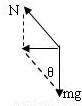
根据牛顿第二定律，得
mgtanθ=m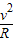
又由数学知识得到
tanθ=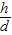
联立解得
v=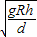
故选B
点评：本题是生活中圆周运动的问题，关键是分析物体的受力情况，确定向心力的来源．
解答：解：设路面的斜角为θ，作出汽车的受力图，如图．
根据牛顿第二定律，得
mgtanθ=m
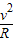
又由数学知识得到
tanθ=
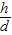
联立解得
v=
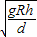
故选B
点评：本题是生活中圆周运动的问题，关键是分析物体的受力情况，确定向心力的来源．
练习册系列答案
黄冈冠军课课练系列答案
相关题目
在高速公路的拐弯处，路面造得外高内低，即当车向右拐弯时，司机左侧的路面比右侧的要高一些，路面与水平面间的夹角为θ设拐弯路段是半径为R的圆弧，要使车速为v时车轮与路面之间的横向（即垂直于前进方向）摩擦力等于零，θ应满足（ ）