题目内容
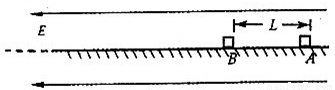
质量均为m=0.1kg的两小滑块A、B,相距L=2m、放在足够长的绝缘水平面上,与水平面间的动摩擦因数均为μ=0.2,A带电量为q=+3×10-3C,B不带电.在水平面附近空间加有水平向左的匀强电场E=l×102v/m,现同时由静止释放A、B,此后A将与B发生多次碰撞,碰撞时间极短且无机械能损失,A带电量保持不变,B始终不带电,g取10m/s2试求(1)A、B第一次碰前瞬间A的速度vA1
(2)A、B第一次碰后瞬间B的速度vB1
(3)小滑块B运动的总路程S.
【答案】分析:(1)由静止释放A后,A在水平方向受到电场力和滑动摩擦力,根据牛顿第二定律求出加速度,由速度位移关系式求出A、B第一次碰前瞬间A的速度vA1.
(2)由于AB碰撞时间极短且无机械能损失,动量和动能均守恒,由两大守恒列方程,求解A、B第一次碰后瞬间B的速度vB1.
(3)A、B质量相等,发生弹性碰撞,将交换速度,经多次碰撞后,AB最终停在在一起.滑动摩擦力做功与小滑块B运动的总路程S成正比,根据能量守恒定律列方程解出小滑块B运动的总路程S.
解答:解:
(1)释放A后的加速度,由牛顿第二定律得:qE-μmg=maA
代入得到,aA=1m/s2
又据公式 =2aAL
=2aAL
得到A、B第一次碰前瞬间A的速度vA1=2m/s.
(2)由题,碰撞时间极短且无机械能损失,根据动量和动能守恒得
mvA1=mvA1′+mvB1
 =
= +
+
解得:mvA1′=0,vB1=vA1=2m/s,由此可知,碰撞后AB两滑块交换速度.
(3)由于每次碰撞两滑块均交换速度,多次碰撞后,最终A、B停在一起.根据能量守恒定律得
Eq(L+S)=μmg(L+S)+μmgS
解得,S=2m
答:
(1)A、B第一次碰前瞬间A的速度vA1=2m/s.
(2)A、B第一次碰后瞬间B的速度vB1=2m/s.
(3)小滑块B运动的总路程S=2m.
点评:本题两滑块多次发生弹性碰撞,质量相等时,交换速度作为重要结论,要在理解的基础上进行识记.
(2)由于AB碰撞时间极短且无机械能损失,动量和动能均守恒,由两大守恒列方程,求解A、B第一次碰后瞬间B的速度vB1.
(3)A、B质量相等,发生弹性碰撞,将交换速度,经多次碰撞后,AB最终停在在一起.滑动摩擦力做功与小滑块B运动的总路程S成正比,根据能量守恒定律列方程解出小滑块B运动的总路程S.
解答:解:
(1)释放A后的加速度,由牛顿第二定律得:qE-μmg=maA
代入得到,aA=1m/s2
又据公式
 =2aAL
=2aAL得到A、B第一次碰前瞬间A的速度vA1=2m/s.
(2)由题,碰撞时间极短且无机械能损失,根据动量和动能守恒得
mvA1=mvA1′+mvB1
 =
= +
+
解得:mvA1′=0,vB1=vA1=2m/s,由此可知,碰撞后AB两滑块交换速度.
(3)由于每次碰撞两滑块均交换速度,多次碰撞后,最终A、B停在一起.根据能量守恒定律得
Eq(L+S)=μmg(L+S)+μmgS
解得,S=2m
答:
(1)A、B第一次碰前瞬间A的速度vA1=2m/s.
(2)A、B第一次碰后瞬间B的速度vB1=2m/s.
(3)小滑块B运动的总路程S=2m.
点评:本题两滑块多次发生弹性碰撞,质量相等时,交换速度作为重要结论,要在理解的基础上进行识记.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
(18分)
(1)(4分)如图,螺旋测微器甲和游标卡尺乙的读数分别为 mm, cm.
(2)(6分)在验证机械能守恒定律的实验中,与纸带相连的质量为1kg的重锤自由下落,打出的纸带如图所示,相邻记数点时间间隔为0.02s,,g取9.8m/s2.求:
①打点计时器打下记数点B时,物体的速度VB= m/s(保留两位有效数字);
②某同学根据纸带上的O点到B点的数据,计算出物体的动能增加量△Ek=0.47J,重力势能减小量△Ep=0.48J,经过多次实验均发现△Ek略小于△Ep,试分析原因: .
(3)(8分)测量一个电阻Rx阻值(约为70Ω),给你如下器材:
| A.电流表(50mA,内阻约10Ω) |
| B.电压表(0-3V-15V内阻分别是3KΩ和15KΩ) |
| C.电源(1.5V干电池2节) |
| D.滑动变阻器R1(0-10Ω) |
F.电键、导线若干
根据所给定的器材和实验要求,画出了实验电路图如图所示,问:

①实验中电压表量程应选择 ,滑动变阻器应选择 (填“R1”或“R2”).
②根据电路图和选择的仪器连接好下面的实物线路图.

 (2008?卢湾区模拟)在科技活动中某同学利用自制的电子秤来称量物体的重力,如图所示,为电子秤的原理图.托盘和弹簧的质量均不计,滑动变阻器的滑动端与弹簧上端连接,当托盘中没有放物体时,电压表示数为零;当托盘中的物体的质量改变时,电压表示数发生改变,从而测出物体的质量.设变阻器的总电阻为R,总长度为l,电源电动势为E,内 阻不计.弹簧产生的弹力与弹簧压缩量x成正比,即F=kx(k为常数),不计一切摩擦和其他阻力,电压表为理想电表.
(2008?卢湾区模拟)在科技活动中某同学利用自制的电子秤来称量物体的重力,如图所示,为电子秤的原理图.托盘和弹簧的质量均不计,滑动变阻器的滑动端与弹簧上端连接,当托盘中没有放物体时,电压表示数为零;当托盘中的物体的质量改变时,电压表示数发生改变,从而测出物体的质量.设变阻器的总电阻为R,总长度为l,电源电动势为E,内 阻不计.弹簧产生的弹力与弹簧压缩量x成正比,即F=kx(k为常数),不计一切摩擦和其他阻力,电压表为理想电表.
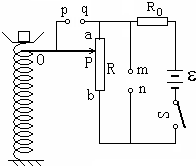 在科技活动中某同学利用自制的电子秤来称量物体的重力,如图所示,为电子秤的原理图.托盘和弹簧的质量均不计,滑动变阻器的滑动端与弹簧上端连接,当托盘中没有放物体时,电压表示数为零;当托盘中的物体的质量改变时,电压表示数发生改变,从而测出物体的质量.设变阻器的总电阻为R,总长度为l,电源电动势为E,内阻为0,弹簧劲度系数为k,弹簧产生的弹力与弹簧压缩量x成正比,即F=k?x.不计一切摩擦和其他阻力,电压表为理想表.
在科技活动中某同学利用自制的电子秤来称量物体的重力,如图所示,为电子秤的原理图.托盘和弹簧的质量均不计,滑动变阻器的滑动端与弹簧上端连接,当托盘中没有放物体时,电压表示数为零;当托盘中的物体的质量改变时,电压表示数发生改变,从而测出物体的质量.设变阻器的总电阻为R,总长度为l,电源电动势为E,内阻为0,弹簧劲度系数为k,弹簧产生的弹力与弹簧压缩量x成正比,即F=k?x.不计一切摩擦和其他阻力,电压表为理想表.


