题目内容
10只相同的轮子并排水平排列,圆心分别为O1、O2、O3…、O10,已知O1O10=3.6m,水平转轴通过圆心,轮子均绕轴以n= r/s的转速顺时针转动.现将一根长L=0.8m、质量为m=2.0kg 的匀质木板平放在这些轮子的左端,木板左端恰好与O1竖直对齐(如图所示),木板与轮缘间的动摩擦因数为μ=0.16.则木板水平移动的总时间为( )
r/s的转速顺时针转动.现将一根长L=0.8m、质量为m=2.0kg 的匀质木板平放在这些轮子的左端,木板左端恰好与O1竖直对齐(如图所示),木板与轮缘间的动摩擦因数为μ=0.16.则木板水平移动的总时间为( )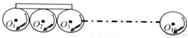
A.1.5
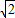 s
sB.2s
C.3s
D.2.5s
【答案】分析:匀质木板平放在轮子的左端时,受到向右的滑动摩擦力作用而向右做匀加速直线运动,根据牛顿第二定律求出木板的加速度,由速度公式求出木板的速度达到轮缘速度时经过的时间,并求出此过程的位移.接下来木板将以与轮缘相等的速度做匀速直线运动,当木板伸出轮子一半长度时木板将离开轮子,确定木板匀速运动的位移,求出匀速运动的时间,再求出总时间.
解答:解:开始阶段匀质木板做匀加速运动,加速度为:a=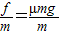 =1.6m/s2
=1.6m/s2
轮缘的速度大小为:v=2πrn,r=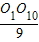 =0.4m,代入解得:v=1.6m/s.
=0.4m,代入解得:v=1.6m/s.
设木板速度与轮缘速度相等经过的时间为t1.则有v=at1,得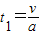 =1s,
=1s,
匀加速运动通过的位移为x1=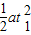 =0.8m
=0.8m
当木板伸出轮子一半长度时木板将离开轮子,所以木板做匀速直线运动的位移为:
x2=O1O10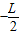 -x1=2.4m
-x1=2.4m
匀速直线运动的时间为t2=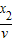 =1.5s
=1.5s
所以木板水平移动的总时间为t=t1+t2=2.5s
故选D
点评:本题中木板的运动情况与物体放在传送带上运动情况相似,就是要注意木板匀速运动的位移,当木板的重心运动到O10的正上方时,木板即将翻倒离开轮子.
解答:解:开始阶段匀质木板做匀加速运动,加速度为:a=
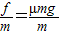 =1.6m/s2
=1.6m/s2轮缘的速度大小为:v=2πrn,r=
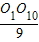 =0.4m,代入解得:v=1.6m/s.
=0.4m,代入解得:v=1.6m/s.设木板速度与轮缘速度相等经过的时间为t1.则有v=at1,得
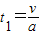 =1s,
=1s,匀加速运动通过的位移为x1=
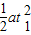 =0.8m
=0.8m当木板伸出轮子一半长度时木板将离开轮子,所以木板做匀速直线运动的位移为:
x2=O1O10
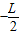 -x1=2.4m
-x1=2.4m匀速直线运动的时间为t2=
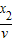 =1.5s
=1.5s所以木板水平移动的总时间为t=t1+t2=2.5s
故选D
点评:本题中木板的运动情况与物体放在传送带上运动情况相似,就是要注意木板匀速运动的位移,当木板的重心运动到O10的正上方时,木板即将翻倒离开轮子.

练习册系列答案
相关题目
 (2012?武汉模拟)10只相同的轮子并排水平排列,圆心分别为O1、O2、O3…、O10,已知O1O10=3.6m,水平转轴通过圆心,轮子均绕轴以n=
(2012?武汉模拟)10只相同的轮子并排水平排列,圆心分别为O1、O2、O3…、O10,已知O1O10=3.6m,水平转轴通过圆心,轮子均绕轴以n= 10只相同的轮子并排水平排列,圆心分别为O1、O2、O3,…O10,已知O1O10=3.6m,水平转轴通过圆心,轮子均绕轴以
10只相同的轮子并排水平排列,圆心分别为O1、O2、O3,…O10,已知O1O10=3.6m,水平转轴通过圆心,轮子均绕轴以
 =
= 的转速顺时针转动.现将一根长L=0.8 m、质量为m=2.0 kg 的匀质木板平放在这些轮子的左端,木板左端恰好与O1竖直对齐(如图所示),木板与轮缘间的动摩擦因数为
的转速顺时针转动.现将一根长L=0.8 m、质量为m=2.0 kg 的匀质木板平放在这些轮子的左端,木板左端恰好与O1竖直对齐(如图所示),木板与轮缘间的动摩擦因数为 =0.16.则木板水平移动的总时间为(
)
=0.16.则木板水平移动的总时间为(
)

 =
= 的转速顺时针转动.现将一根长L=0.8 m、质量为m=2.0 kg 的匀质木板平放在这些轮子的左端,木板左端恰好与O1竖直对齐(如图所示),木板与轮缘间的动摩擦因数为
的转速顺时针转动.现将一根长L=0.8 m、质量为m=2.0 kg 的匀质木板平放在这些轮子的左端,木板左端恰好与O1竖直对齐(如图所示),木板与轮缘间的动摩擦因数为 =0.16.则木板水平移动的总时间为( D )
=0.16.则木板水平移动的总时间为( D )
 B.2s
B.2s