题目内容
 如图所示,A、B在同一水平线上,以A_B为直径的半圆周与竖直光滑绝缘杆相交于M点.电荷量为Q1、Q2的两个正、负点电荷分别固定在A点和B点,一个带正电的轻金属环q(视为点电荷,且重力忽略不计)套在绝缘杆上,在M点恰好平衡,MA与AB的夹角为α,则( )
如图所示,A、B在同一水平线上,以A_B为直径的半圆周与竖直光滑绝缘杆相交于M点.电荷量为Q1、Q2的两个正、负点电荷分别固定在A点和B点,一个带正电的轻金属环q(视为点电荷,且重力忽略不计)套在绝缘杆上,在M点恰好平衡,MA与AB的夹角为α,则( )分析:带正电的轻金属环q在M点恰好平衡,分析受力情况,根据平衡条件和库仑定律求解.
解答:解:设圆周的直径为d,根据库仑定律得:
Q1对q的库仑力大小为F1=k
Q2对q的库仑力大小为F2=k
对q,根据平衡条件得:F1sinα=F2cosα
联立以上三式得:tan3α=
故选A
Q1对q的库仑力大小为F1=k
| Q1q |
| (dcosα)2 |
Q2对q的库仑力大小为F2=k
| Q2q |
| (dsinα)2 |
对q,根据平衡条件得:F1sinα=F2cosα
联立以上三式得:tan3α=
| Q2 |
| Q1 |
故选A
点评:本题是库仑定律与平衡条件的综合应用,同时运用到几何知识分析两点与q之间距离关系,即可得到解答.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
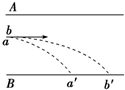 如图所示,a、b两个带正电的粒子,以相同的速度先后垂直于电场线从同一点进入平行板间的匀强电场后,a粒子打在B板的a′点,b粒子打在B板的b′点,若不计重力,则( )
如图所示,a、b两个带正电的粒子,以相同的速度先后垂直于电场线从同一点进入平行板间的匀强电场后,a粒子打在B板的a′点,b粒子打在B板的b′点,若不计重力,则( )| A、a的电荷量一定大于b的电荷量 | B、b的质量一定大于a的质量 | C、a的比荷一定大于b的比荷 | D、b的比荷一定大于a的比荷 |
 如图所示,A、B两物体均重G=10N,各接触面间的动摩擦因数均为μ=0.3,同时有F=1N的两个水平力分别作用在A和B上,则地面对B的摩擦力等于( ),B对A的摩擦力等于( )
如图所示,A、B两物体均重G=10N,各接触面间的动摩擦因数均为μ=0.3,同时有F=1N的两个水平力分别作用在A和B上,则地面对B的摩擦力等于( ),B对A的摩擦力等于( ) (2013?凉山州模拟)如图所示,A、B、C是三个物体同时同地开始运动的位移时间图象,在时间t0内下列说法正确的是( )
(2013?凉山州模拟)如图所示,A、B、C是三个物体同时同地开始运动的位移时间图象,在时间t0内下列说法正确的是( )
 B.
B. C.
C. D.
D.
