题目内容
在图甲中A和B是真空中的两块面积很大的平行金属板，A、B问的电压U邶随时间变化的规律如图乙所示，在图甲中O点到A和B的距离皆为l，在O处不断地产生电荷量为叭质量为m的带负电的微粒，不计重力，不考虑微粒之间的相互作用，这种微粒产生后，从静止出发在电场力的作用下运动，设微粒一旦碰到金属板，就附在板上不再运动，且其电量同时消失，不影响A、B板的电势。已知交变电压的周期T=6.0×10-3 s。正电压为U0，负电压为-2U0，且U0=3.0×102V，微粒电荷量q=2.0×10-7 C，质量m=1.0×10-9 kg，l=0.3 m。试求：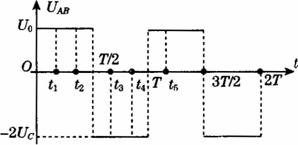
(1)在t=0时刻从静止出发的微粒，会在t1时刻到达极板，求t1的值?
(2)若在t=0到t=T／2这段时间内的某一时刻t2产生的微粒刚好不能到达A板，求t2的值?
(3)求t2时刻产生的微粒到达B板所需的时间?
解：(1)设在t=0时刻产生的微粒在t1时刻到达A板，且t1＞T／2.
在此过程中微粒加速度a1=
m／s2=1×105 m／s2
由l=
得：t1=
×10-3 s=2.45×10-3 s
t1＜T／2，所以假设成立，该微粒在t1=2.45×10-3 s的时刻到达A板。
(2)设在t=0到t=T／2这段时间内的t2时刻产生的微粒刚好不能到达A板，若再设此微粒在T／2～T时间内的t3时刻以达A板时的速度刚好为零。T/2～t3时间内的加速度的大小为：
a2=
=2×105 m／s2
微粒在T／2时刻的速度
u1=a1(
-t2)=a2(t3
)
微粒在t2～t3时间内的位移
l=
a1(
-t2)2+
a2(t3
)2
联立解得：t2=1×10-3 s，t3=4×10-3 s＜T，所以假设成立，t2=1×10-3 s时刻产生的微粒刚好不能到达A极板。
(3)t2时刻产生的微粒在t3时刻到达A板时速度为零，并立即返回，在t3～T时间内向B板运动，加速度为a2，则其位移s1为：
s1=
a2(T-T3)2=
×2×105×(6.0×10-3-4.0×10-3)2=0.4m＜2l
此时速度v1=a2(T-t3)=400 m／s
接着微粒以加速度a1向左减速运动，设运动时间为t，由运动学公式s2=v1t
a1t2有：
0.2=400t
×1×105 t2
解得：t=(4
)×10-3=0.536×10-3 s＜
别解t=(4+
)×10-3舍去
故t2时刻产生的微粒到达B板所需的时间
t0=(T-t2)+t=5.536×10-3 s
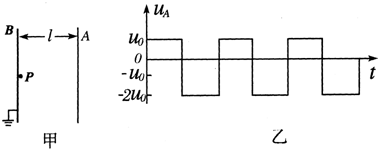（T/2）2/16m，若在交流电压变化的每个周期T内，平均产生400个上述微粒．求（不计重力，不考虑微粒之间的相互作用）：
