题目内容
如图甲所示,A、B是真空中的两块面积很大的平行金属板,相距为L,加上周期为了的交流电压,在两板间产生交变的匀强电场.已知B板的电势为零,A板的电势UA随时间变化的规律如图乙所示,其中UA最大值为U,最小值为-2U.在靠近B板的P点处,不断地产生电量为q、质量为m的带负电的微粒,各个时刻产生带电微粒的机会均等,这种微粒产生后,从静止出发在电场力的作用下运动,设微粒一旦碰到金属板,它就附在板上不再运动,且其电量同时消失,不影响A、B板的电压.已知上述的T、U、L、g和m等各量正好满足等式L2=3Uq(T/2)2/16m,若在交流电压变化的每个周期T内,平均产生400个上述微粒.求(不计重力,不考虑微粒之间的相互作用):(1)从t=0开始运动的微粒到达A板所用的时间.
(2)在t=0到tc=T/2这段时间内产生的微粒中,有多少个微粒可到达A板.

【答案】分析:(1)粒子在电场中在电场力的作用下线加速,根据粒子的运动的距离求运动的时间.
(2)粒子先加速运动再减速运动,到达A板时速度恰好见为零,此时是恰好还能到达A的粒子,在此之前的粒子都可以到达A板.
解答:解:(1)当电压为U时,粒子的加速度为:a1= ,
,
当电压为-2U时,粒子的加速度为:a2=- =-2a1…①
=-2a1…①
用a1= 代入已知式L2=3Uq
代入已知式L2=3Uq (
( )2,
)2,
解得:l=3a1 (
( )2…②
)2…②
在t=0时刻加速运动的粒子,经 T时间的位移为:
T时间的位移为:
L= a1(
a1( T)2>l…③
T)2>l…③
说明从静止开始运动的微粒到达A板的时间小于 T,
T,
所以,从t=0开始运动的微粒到达A板时一直处于加速状态,且加速度为a1,到达A板的时间为:
t= =
= .
.
(2)设在0~ T时间内,在t=t1时刻开始运动的粒子经△t1时间在电压为U加速,然后在电压为-2U减速一段时间到达A板,
T时间内,在t=t1时刻开始运动的粒子经△t1时间在电压为U加速,然后在电压为-2U减速一段时间到达A板,
设加速阶段位移为d1,减速阶段运动位移为d2,则
l=d1-d2…④
d1= a1(△t1)2 …⑤
a1(△t1)2 …⑤
d2=(0-υ12) =(0-(a1△t1)2)
=(0-(a1△t1)2) …⑥
…⑥
联立①②④⑤⑥解得△t1= T
T
t1= T-△t1=
T-△t1= T
T
即从0~ T时间内产生的粒子均可到达A板,设0~
T时间内产生的粒子均可到达A板,设0~ T时间内产生的粒子有n个粒子到达A板,则n=
T时间内产生的粒子有n个粒子到达A板,则n= ×
× =100(个).
=100(个).
答:(1)从t=0开始运动的微粒到达A板所用的时间为 .
.
(2)在t=0到tc= T这段时间内产生的微粒中,有100个微粒可到达A板.
T这段时间内产生的微粒中,有100个微粒可到达A板.
点评:本题中粒子的运动的过程比较复杂,粒子在电场中先加速运动再减速运动,到达A板时速度恰好见为零,此时是恰好还能到达A的粒子.
(2)粒子先加速运动再减速运动,到达A板时速度恰好见为零,此时是恰好还能到达A的粒子,在此之前的粒子都可以到达A板.
解答:解:(1)当电压为U时,粒子的加速度为:a1=
 ,
,当电压为-2U时,粒子的加速度为:a2=-
 =-2a1…①
=-2a1…①用a1=
 代入已知式L2=3Uq
代入已知式L2=3Uq (
( )2,
)2,解得:l=3a1
 (
( )2…②
)2…②在t=0时刻加速运动的粒子,经
 T时间的位移为:
T时间的位移为:L=
 a1(
a1( T)2>l…③
T)2>l…③说明从静止开始运动的微粒到达A板的时间小于
 T,
T,所以,从t=0开始运动的微粒到达A板时一直处于加速状态,且加速度为a1,到达A板的时间为:
t=
 =
= .
.(2)设在0~
 T时间内,在t=t1时刻开始运动的粒子经△t1时间在电压为U加速,然后在电压为-2U减速一段时间到达A板,
T时间内,在t=t1时刻开始运动的粒子经△t1时间在电压为U加速,然后在电压为-2U减速一段时间到达A板,设加速阶段位移为d1,减速阶段运动位移为d2,则
l=d1-d2…④
d1=
 a1(△t1)2 …⑤
a1(△t1)2 …⑤d2=(0-υ12)
 =(0-(a1△t1)2)
=(0-(a1△t1)2) …⑥
…⑥联立①②④⑤⑥解得△t1=
 T
T t1=
 T-△t1=
T-△t1= T
T 即从0~
 T时间内产生的粒子均可到达A板,设0~
T时间内产生的粒子均可到达A板,设0~ T时间内产生的粒子有n个粒子到达A板,则n=
T时间内产生的粒子有n个粒子到达A板,则n= ×
× =100(个).
=100(个).答:(1)从t=0开始运动的微粒到达A板所用的时间为
 .
.(2)在t=0到tc=
 T这段时间内产生的微粒中,有100个微粒可到达A板.
T这段时间内产生的微粒中,有100个微粒可到达A板.点评:本题中粒子的运动的过程比较复杂,粒子在电场中先加速运动再减速运动,到达A板时速度恰好见为零,此时是恰好还能到达A的粒子.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
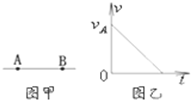 如图甲所示,A、B是一条电场线上的两点,当一个电子以某一初速度只在电场力作用下沿AB由A点运动到B点,其速度-时间图象如图乙所示,电子到达B点时速度恰为零.下列判断正确的是( )
如图甲所示,A、B是一条电场线上的两点,当一个电子以某一初速度只在电场力作用下沿AB由A点运动到B点,其速度-时间图象如图乙所示,电子到达B点时速度恰为零.下列判断正确的是( ) 如图甲所示,A、B 是一对平行金属板. A 板的电势φA=0,B 板的电势φB随时间的变化规律为如图乙所示,现有一电子从 A 板上的小孔进入板间的电场区内.电子的初速度和重力的影响均可忽略,则( )
如图甲所示,A、B 是一对平行金属板. A 板的电势φA=0,B 板的电势φB随时间的变化规律为如图乙所示,现有一电子从 A 板上的小孔进入板间的电场区内.电子的初速度和重力的影响均可忽略,则( ) 如图甲所示,A、B是叠放在光滑水平面上的两物块,两物块质量均为m,水平力F作用在物块B上,A、B一起从静止开始做直线运动(无相对滑动),F随时间t变化关系如图乙所示.下列说法正确的是( )
如图甲所示,A、B是叠放在光滑水平面上的两物块,两物块质量均为m,水平力F作用在物块B上,A、B一起从静止开始做直线运动(无相对滑动),F随时间t变化关系如图乙所示.下列说法正确的是( )
 (2013?马鞍山三模)Ⅰ在《验证力的平行四边形定则》的实验中,某同学的实验情况如图甲所示,其中A为固定橡皮筋的图钉,O为橡皮条与细绳的结点,OB和OC为细绳.图乙是在白纸上根据实验结果画出的图,则:
(2013?马鞍山三模)Ⅰ在《验证力的平行四边形定则》的实验中,某同学的实验情况如图甲所示,其中A为固定橡皮筋的图钉,O为橡皮条与细绳的结点,OB和OC为细绳.图乙是在白纸上根据实验结果画出的图,则: