题目内容
轻杆长2L,中点装在水平轴O点,两端分别固定着小球A和B,A球质量为m,B球质量为2m,小球的尺寸大小忽略不计,杆在竖直平面内做圆周运动.(1)当杆绕O转动到某一速度时,A球在最高点(如图所示),此时杆OA恰好不受力.求此时O轴的受力大小和方向;

(2)保持上一问中的速度,B球运动到最高点时,求O轴的受力大小和方向;
(3)在杆的转速逐渐变化的过程中,能否出现O轴不受力的情况?此时A和B的状态各如何?
答案:
解析:
提示:
解析:
| (1)T=4mg,方向向下;(2)T=2mg,方向向下;(3)当A、B两球以角速度ω= |
提示:
| 提示:(1)A球在最高点时,OA恰好不受力,说明A球的重力提供向心力,有mg=m 以上两式得.T=4mg.由牛顿第三定律得,球对杆的拉力T′=4mg,杆对O轴的作用力大小为4mg,方向向下. (2)B球在最高点,有速度ν= (3)要使O轴不受力,由于mB>mA,所以B球应在最上端,A球在最下端.设O轴不受力时球的速度为ν′,对A球:T1-mg=m |

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
 如图所示,轻杆长2l,中点装在水平轴O点,两端分别固定着小球A和B,A球质量为m,B球
如图所示,轻杆长2l,中点装在水平轴O点,两端分别固定着小球A和B,A球质量为m,B球 如图所示,轻杆长2l,中点装在水平轴O点,两端分别固定着小球A和B,A球质量为m,B球质量为2m,两者一起在竖直平面内绕O轴做圆周运动.若B球运动到最高点时的速度等于
如图所示,轻杆长2l,中点装在水平轴O点,两端分别固定着小球A和B,A球质量为m,B球质量为2m,两者一起在竖直平面内绕O轴做圆周运动.若B球运动到最高点时的速度等于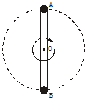 如图所示,轻杆长2l,中点装在水平轴O点,两端分别固定着小球A和B,A球质量为m,B球质量为2m,两者一起在竖直平面内绕O轴做圆周运动.
如图所示,轻杆长2l,中点装在水平轴O点,两端分别固定着小球A和B,A球质量为m,B球质量为2m,两者一起在竖直平面内绕O轴做圆周运动.
