题目内容
如图所示，轻杆长2l，中点装在水平轴O点，两端分别固定着小球A和B，A球质量为m，B球质量为2m，两者一起在竖直平面内绕O轴做圆周运动．若B球运动到最高点时的速度等于| 3gl |
0
0
（g为重力加速度）分析：当B球运动到最高点时，先以B球为研究对象，根据牛顿第二定律求出杆对B球的作用力大小和方向．再以A球研究对象，根据牛顿第二定律求出杆对A球的作用力大小和方向，就能分析杆对O轴的作用力了．
解答：解：设杆对B球的作用力大小为F1、方向向下，杆对A球的作用力大小为F2．
根据牛顿第二定律，得
对B球：2mg+F1=2m
，
又v=
代入得F1=4mg，方向向下；
对A球：F2-mg=m
解得 F2=4mg，方向向上
则杆对O轴的作用力为F=F1-F2=4mg-4mg=0
故答案为：0
根据牛顿第二定律，得
对B球：2mg+F1=2m
| v2 |
| l |
又v=
| 3gl |
代入得F1=4mg，方向向下；
对A球：F2-mg=m
| v2 |
| l |
解得 F2=4mg，方向向上
则杆对O轴的作用力为F=F1-F2=4mg-4mg=0
故答案为：0
点评：本题是双球圆周运动的类型，采用隔离法研究，关键要分析受力，确定向心力的来源．
练习册系列答案
一线名师权威作业本系列答案
相关题目
如图所示，轻杆长2l，中点装在水平轴O点，两端分别固定着小球A和B，A球质量为m，B球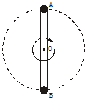
如图所示，轻杆长2l，中点装在水平轴O点，两端分别固定着小球A和B，A球质量为m，B球质量为2m，两者一起在竖直平面内绕O轴做圆周运动．
