题目内容
一个内壁光滑的圆锥筒的轴线是竖直的,圆锥固定,有质量相同的两个小球A和B贴着筒的内壁在水平面内做匀速圆周运动,如图所示,A的运动半径较大.则
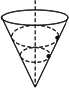
A.A球的角速度必小于B球的角速度
B.A球的线速度必小于B球的线速度
C.A球的运动周期必大于B球的运动周期
D.A球对筒壁的压力必大于B球对筒壁的压力
答案:AC
解析:
提示:
解析:
|
求解匀速圆周运动的向心力常用以下两种方法:(1)先对物体进行受力分析,画好受力图,然后用求合力的方法得到指向圆心的向心力; (2)借助于v、ω、T、n和r等量求得a向,再用牛顿第二定律F向=ma向求得向心力. 本题中两球均贴着筒的内壁在水平面内做匀速圆周运动,它们均受到重力和筒壁对它的弹力作用,这两个力的合力提供向心力,如图所示,可知筒壁对小球的弹力FN=mg/sin 由牛顿第二定律,可得 mgcot 所以:ω= T=2π 由以上四个表示式可知:①ωA<ωB②vA>vB③TA>TB④FNA=FNB.所以选项AC正确.
|
提示:
|
处理圆周运动的动力学问题时,在明确研究对象以后,首先要注意两个问题: (1)确定研究对象运动的轨道平面和圆心的位置,以便确定向心力的方向.例如本题小球在水平面上做匀速圆周运动,小球做圆周运动的圆心就在同一水平面上. (2)向心力是根据力的效果命名的,在分析做圆周运动的质点受力的情况时,切不可在物体的相互作用(重力、弹力、摩擦力等)以外再添加一个向心力. |

练习册系列答案
相关题目
 如图所示,一个内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,有两个质量相同的小球A和小球B紧贴圆锥筒内壁分别在水平面内做匀速圆周运动,则下列说法中正确的是( )
如图所示,一个内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,有两个质量相同的小球A和小球B紧贴圆锥筒内壁分别在水平面内做匀速圆周运动,则下列说法中正确的是( )| A、A球的线速度必定小于B球的线速度 | B、A球的角速度必定大于B球的角速度 | C、A球运动的周期必定大于B球的周期 | D、A球对筒壁的压力必定大于B球对筒壁的压力 |
 如图所示,一个内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,有两个质量相同的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动,则下列说法不正确的是( )
如图所示,一个内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,有两个质量相同的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动,则下列说法不正确的是( )| A、球A的线速度必定大于球B的线速度 | B、球A的角速度必定等于球B的角速度 | C、球A的运动周期必定小于球B的运动周期 | D、球A对筒壁的压力必定大于球B对筒壁的压力 |
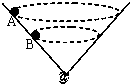 如图所示,一个内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,有两个质量相同的小球A和B紧贴着内壁分别在图中所示位置的水平面内作匀速率圆周运动,则以下判断正确的是( )
如图所示,一个内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,有两个质量相同的小球A和B紧贴着内壁分别在图中所示位置的水平面内作匀速率圆周运动,则以下判断正确的是( )| A、球A的线速度大于球B的线速度 | B、球A的向心加速度小于球B的向心加速度 | C、球A对筒壁的压力等于球B对筒壁的压力 | D、球A的运动周期大于球B的运动周期 |
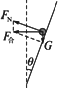
 如图所示,一个内壁光滑的圆锥筒的轴线是竖直的,圆锥固定,有质量相同的两个小球A和B贴着筒的内壁在水平面内做匀速圆周运动,A的运动半径较大,则( )
如图所示,一个内壁光滑的圆锥筒的轴线是竖直的,圆锥固定,有质量相同的两个小球A和B贴着筒的内壁在水平面内做匀速圆周运动,A的运动半径较大,则( ) 如图所示,一个内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,两个质量相同的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动,则vA
如图所示,一个内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,两个质量相同的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动,则vA