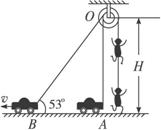
题目内容
如图
图
解析:铁链脱落的过程中机械能守恒.我们可以选定某一个参考平面,找出铁链初末状态的机械能列守恒方程求解.也可以利用等效法求解:铁链要脱离滑轮时重力势能的减少,等效于将图中滑轮左边铁链部分移至右边铁链部分下端时重力势能的减少.然后由ΔEp=ΔEk列方程.
解法一:(利用E2=E1求解):设铁链单位长度的质量为ρ,且选取初始位置铁链的下端A、B所在的水平面为参考平面,则铁链初态的机械能为
E1=ρLg![]() =
=![]() ρgL2
ρgL2
末态的机械能为E2=![]() mv2=
mv2=![]() ρLv2
ρLv2
根据机械能守恒定律有E2=E1
即![]() ρLv2=
ρLv2=![]() ρgL2
ρgL2
解得铁链刚脱离滑轮时的速度v=![]() .
.
解法二:(利用ΔEk=-ΔEp求解):如图

图
-ΔEp=![]() ρLg·
ρLg·![]() =
=![]() ρgL2
ρgL2
动能的增加量ΔEk=![]() ρLv2
ρLv2
根据机械能守恒定律有ΔEk=-ΔEp
即![]() ρLv2=
ρLv2=![]() ρgL2
ρgL2
解得铁链刚脱离滑轮时的速度v=![]()
故铁链刚脱离滑轮时的速度为![]() .
.

练习册系列答案
相关题目