题目内容
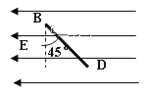
【题目】如图所示,在![]() 平面的第一象限有一匀强电场,电场的方向平行于
平面的第一象限有一匀强电场,电场的方向平行于![]() 轴向下;在
轴向下;在![]() 轴和第四象限的射线
轴和第四象限的射线![]() (
(![]() 与
与![]() 轴的夹角为
轴的夹角为![]() )之间有一匀强磁场,磁感应强度的大小为
)之间有一匀强磁场,磁感应强度的大小为![]() ,方向垂直于纸面向外。有一质量为
,方向垂直于纸面向外。有一质量为![]() ,带有电荷量
,带有电荷量![]() 的粒子由电场左侧平行于
的粒子由电场左侧平行于![]() 轴射入电场。粒子到达
轴射入电场。粒子到达![]() 轴上
轴上![]() 点时,速度方向与
点时,速度方向与![]() 轴的夹角也为φ,
轴的夹角也为φ,![]() 点与原点
点与原点![]() 的距离为d,接着粒子进入磁场,并垂直于
的距离为d,接着粒子进入磁场,并垂直于![]() 飞离磁场。不计粒子重力影响。
飞离磁场。不计粒子重力影响。
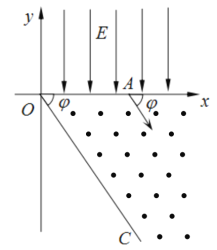
求:(1)粒子在磁场中运动的速度大小;(2)匀强电场的场强大小;(3)粒子水平进入电场时距离原点![]() 的距离.
的距离.
【答案】(1)![]() (2)
(2)![]() (3)
(3) ![]()
【解析】
(1)粒子在磁场中做匀速圆周运动,结合几何关系由洛仑兹力充当向心力可求得粒子在磁场中的速度;
(2)粒子在电场中做的是类平抛运动,对水平方向的匀速和竖直方向的匀加速分中别进行分析,根据牛顿第二定律及运动学公式可求得电场强度;
(3)根据运动学公式,结合加速度,即可求解。
(1) 画出粒子在磁场中运动的轨迹如图所示
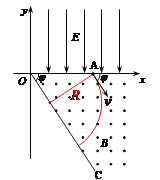
由几何关系得:R=dsinφ①
由洛伦兹力公式和牛顿第二定律得:
![]() ②
②
解得:v=![]() ③;
③;
(2) 质点在电场中作类平抛运动.设质点射入电场的速度为v0,在电场中的加速度为a,运动时间为t,
则有:v0=vcosφ④
vsinφ=at⑤
d=v0t⑥
解得:![]()
设电场强度的大小为E,由牛顿第二定律得:
qE=ma⑦
③~⑦式联立,解得:![]() ;
;
(3) 设粒子入射点位于y轴正方向的D点,距离原点O为L,
粒子在竖直方向做匀加速直线运动:![]() ⑧
⑧
⑥~⑧式联立,解得:![]() 。
。

练习册系列答案
相关题目