题目内容
如图甲所示,用一轻质绳拴着一质量为m的小球,在竖直平面内做圆周运动(不计一切阻力),小球运动到最高点时绳对小球的拉力为T,小球在最高点的速度大小为v,其T-v2图象如图乙所示,则( )

分析:小球在竖直面内做圆周运动,到最高点时由绳对小球的拉力和重力的合力提供向心力,根据图象、应用向心力公式、牛顿第二定律分析答题.根据牛顿第二定律和机械能守恒列式求解小球在最低点和最高点时绳的拉力差.
解答:解:在最高点时,绳对小球的拉力和重力的合力提供向心力,则得:
mg+T=m
得 T=
?v2-mg ①
由图象知,T=0时,v2=b.图象的斜率k=
,则得:
=
,得:绳长 L=
;
当v2=0时,T=-a,由①得:-a=-mg,得 g=
;
当v2=c时,代入①得:T=
?c-mg=
?c+a;
只要v2≥b,绳子的拉力大于0,根据牛顿第二定律得:
最高点:T1+mg=m
②
最低点:T2-mg=m
③
从最高点到最低点的过程中,根据机械能守恒定律得:
m
-
m
=2mgL ④
联立②③④解得:T2-T1=6mg,即小球在最低点和最高点时绳的拉力差均为6a,故ABC错误,D正确.
故选:D
mg+T=m
| v2 |
| L |
得 T=
| m |
| L |
由图象知,T=0时,v2=b.图象的斜率k=
| b |
| a |
| m |
| L |
| b |
| a |
| ma |
| b |
当v2=0时,T=-a,由①得:-a=-mg,得 g=
| a |
| m |
当v2=c时,代入①得:T=
| m |
| L |
| b |
| a |
只要v2≥b,绳子的拉力大于0,根据牛顿第二定律得:
最高点:T1+mg=m
| ||
| L |
最低点:T2-mg=m
| ||
| L |
从最高点到最低点的过程中,根据机械能守恒定律得:
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
| v | 2 1 |
联立②③④解得:T2-T1=6mg,即小球在最低点和最高点时绳的拉力差均为6a,故ABC错误,D正确.
故选:D
点评:本题主要考查了圆周运动向心力公式的直接应用,要求同学们能根据图象获取有效信息.

练习册系列答案
相关题目

 如图甲所示,水平平台的右端安装有轻质滑轮,质量为M=2.5kg的物块A放在与滑轮相距l的平台上,现有一轻绳跨过定滑轮,左端与物块连接,右端挂质量为m=0.5kg的小球B,绳拉直时用手托住小球使其在距地面h高处静止,绳与滑轮间的摩擦不计,重力加速度为g(g取10 m/s2).设最大静摩擦力等于滑动摩擦力.
如图甲所示,水平平台的右端安装有轻质滑轮,质量为M=2.5kg的物块A放在与滑轮相距l的平台上,现有一轻绳跨过定滑轮,左端与物块连接,右端挂质量为m=0.5kg的小球B,绳拉直时用手托住小球使其在距地面h高处静止,绳与滑轮间的摩擦不计,重力加速度为g(g取10 m/s2).设最大静摩擦力等于滑动摩擦力.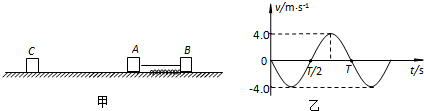 (1)物体B运动速度的最大值;
(1)物体B运动速度的最大值;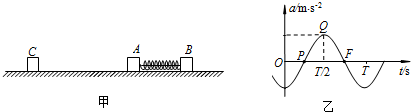 计时,得到物体A的加速度?时间图象如图乙所示,且已知PQFP所包围的曲面面积的数值恰好为8.求:
计时,得到物体A的加速度?时间图象如图乙所示,且已知PQFP所包围的曲面面积的数值恰好为8.求: