题目内容
4.如图甲所示,一对足够长的平行粗糙导轨固定在与水平面夹角为37°的斜面上,两导轨间距为l=1m,下端接有R=3Ω的电阻,导轨的电阻忽略不计;一根质量m=0.5kg、电阻r=1Ω(导轨间部分)的导体杆垂直静置与两导轨上,并与两导轨接触良好;整个装置处于磁感应强度大小B=2T、垂直于导轨平面向上的匀强磁场中;现用平行于斜面向上的拉力F拉导体杆,拉力F与时间t的关系如图乙所示,导体杆恰好做匀加速直线运动;重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8;求导体杆的加速度大小和导体杆与导轨间的动摩擦因数μ.
分析 导体杆做匀加速直线运动,根据v=at、E=Blv、I=$\frac{E}{R+r}$、F安=BIl求出安培力与时间的关系式,再由牛顿第二定律列式得到F与t的表达式,结合图象的信息,即可求解.
解答 解:设导体杆的加速度大小为a,则t时刻导体杆的速度大小为 v=at
产生的感应电动势为 E=Blv
电路中的感应电流为 I=$\frac{E}{R+r}$=$\frac{Blv}{R+r}$
导体杆上所受的安培力大小为 F安=BIl=$\frac{{B}^{2}{l}^{2}at}{R+r}$
由牛顿第二定律可知:F-mgsin37°-μmgcos37°-$\frac{{B}^{2}{l}^{2}at}{R+r}$=ma
代入数据解得:F=3+$\frac{1}{2}$a+4μ+at(N)
由题图乙有 F=6+2t(N)
比较两式可知:a=2m/s2,μ=0.5
答:导体杆的加速度大小是2m/s2,导体杆与导轨间的动摩擦因数μ是0.5.
点评 本题根据法拉第电磁感应定律、牛顿第二定律、闭合电路欧姆定律和安培力公式推导出安培力与速度的关系式是解决本题的关键,要在图象寻找有价值的信息,结合数学知识研究这类问题.

练习册系列答案
相关题目
3.某一物体从静止开始做直线运动,其加速度随时间变化的图线如图所示,则该物体( )

| A. | 第1s内加速运动,第2、3s内减速运动,第3s末回到出发点 | |
| B. | 第1s末和第4s末速度都是8m/s | |
| C. | 在0-4s内,运动方向保持不变 | |
| D. | 第3s末速度为零,且此时开始改变运动方向 |
4.一列火车和一辆汽车沿同一方向做匀变速直线运动,速度分别为v1和v2.t=0时刻,火车在汽车前方26m处,此后v1、v2在各个时刻的大小如表所示.根据表格中的数据,通过计算求:
(1)两车经过多长时间相距最大?此时最大间距是多少?
(2)经过多长时间两车相遇?
(3)两车初始间距满足什么条件可以相遇两次.
| t/s | 0 | 1 | 2 | 3 | 4 | 5 |
| v1/m•s-1 | 16.0 | 14.0 | 12.0 | 10.0 | … | … |
| v2/m•s-1 | 4.0 | 5.0 | 6.0 | 7.0 | … | … |
(2)经过多长时间两车相遇?
(3)两车初始间距满足什么条件可以相遇两次.
1.在真空中两个点电荷A、B相距10cm,A的带电荷量是B的带电荷量的10倍,B受的库仑力是0.1N,则A受到的库仑力是( )
| A. | 1 N | B. | 0.1 N | C. | 10 N | D. | 100 N |
8. 如图(a),直线MN表示某电场中一条电场线,a、b是线上的两点,将一带负电荷的粒子从a点处由静止释放,粒子从a运动到b过程中的v-t,图象如图(b)所示,设a、b两点的电势分别为φa,φb,场强大小分别为Ea,Eb,粒子在a、b两点的电势能分别为E${\;}_{{p}_{a}}$,E${\;}_{{p}_{b}}$,不计重力,则有( )
如图(a),直线MN表示某电场中一条电场线,a、b是线上的两点,将一带负电荷的粒子从a点处由静止释放,粒子从a运动到b过程中的v-t,图象如图(b)所示,设a、b两点的电势分别为φa,φb,场强大小分别为Ea,Eb,粒子在a、b两点的电势能分别为E${\;}_{{p}_{a}}$,E${\;}_{{p}_{b}}$,不计重力,则有( )
 如图(a),直线MN表示某电场中一条电场线,a、b是线上的两点,将一带负电荷的粒子从a点处由静止释放,粒子从a运动到b过程中的v-t,图象如图(b)所示,设a、b两点的电势分别为φa,φb,场强大小分别为Ea,Eb,粒子在a、b两点的电势能分别为E${\;}_{{p}_{a}}$,E${\;}_{{p}_{b}}$,不计重力,则有( )
如图(a),直线MN表示某电场中一条电场线,a、b是线上的两点,将一带负电荷的粒子从a点处由静止释放,粒子从a运动到b过程中的v-t,图象如图(b)所示,设a、b两点的电势分别为φa,φb,场强大小分别为Ea,Eb,粒子在a、b两点的电势能分别为E${\;}_{{p}_{a}}$,E${\;}_{{p}_{b}}$,不计重力,则有( )| A. | φa>φb | B. | Ea>Eb | ||
| C. | E${\;}_{{p}_{a}}$<E${\;}_{{p}_{b}}$ | D. | 无法比较Ea,Eb的大小关系 |
9. 某同学对四个电阻各进行了一次测量,把每个电阻两端的电压和通过它的电流在U-I坐标系中描点,如图所示的a、b、c、d所示( )
某同学对四个电阻各进行了一次测量,把每个电阻两端的电压和通过它的电流在U-I坐标系中描点,如图所示的a、b、c、d所示( )
 某同学对四个电阻各进行了一次测量,把每个电阻两端的电压和通过它的电流在U-I坐标系中描点,如图所示的a、b、c、d所示( )
某同学对四个电阻各进行了一次测量,把每个电阻两端的电压和通过它的电流在U-I坐标系中描点,如图所示的a、b、c、d所示( )| A. | a的电阻大于d的电阻 | B. | b的电阻大于c的电阻 | ||
| C. | c的电阻大于d的电阻 | D. | d的电阻大于a的电阻 |
16.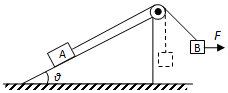 斜面放置于粗糙水平地面上,物块A通过跨过光滑定滑轮的轻质细绳与物块B连接,一水平力F作用于B上,整个系统处于静止状态,如图所示.现保持F方向不变,使B缓慢地移动到滑轮的正下方,该过程中A与斜面始终保持静止,在此过程中( )
斜面放置于粗糙水平地面上,物块A通过跨过光滑定滑轮的轻质细绳与物块B连接,一水平力F作用于B上,整个系统处于静止状态,如图所示.现保持F方向不变,使B缓慢地移动到滑轮的正下方,该过程中A与斜面始终保持静止,在此过程中( )
 斜面放置于粗糙水平地面上,物块A通过跨过光滑定滑轮的轻质细绳与物块B连接,一水平力F作用于B上,整个系统处于静止状态,如图所示.现保持F方向不变,使B缓慢地移动到滑轮的正下方,该过程中A与斜面始终保持静止,在此过程中( )
斜面放置于粗糙水平地面上,物块A通过跨过光滑定滑轮的轻质细绳与物块B连接,一水平力F作用于B上,整个系统处于静止状态,如图所示.现保持F方向不变,使B缓慢地移动到滑轮的正下方,该过程中A与斜面始终保持静止,在此过程中( )| A. | 斜面对物块A的摩擦力一直减小 | B. | 绳对滑轮的作用力保持不变 | ||
| C. | 地面对斜面的摩擦力一直减小 | D. | 地面对斜面的支持力保持不变 |
13.在物理学的发展过程中,许多物理学家的科学发现推动了人类历史的进步.在对以下几位物理学家所作科学贡献的叙述中,正确的说法是( )
| A. | 库仑发现了电流的磁效应 | |
| B. | 麦克斯韦建立了完整的电磁场理论并首先验证了电磁波存在 | |
| C. | 法拉第发现了磁场产生电流的条件和规律 | |
| D. | 伽利略提出的万有引力定律奠定了天体力学的基础 |
14. 在真空中有两个等量的正电荷q1和q2,分别固定于A、B两点,DC为AB连线的中垂线,C为A、B两点连线的中点,将一正电荷q3由C点沿着中垂线移至无穷远处的过程中,下列结论正确的有( )
在真空中有两个等量的正电荷q1和q2,分别固定于A、B两点,DC为AB连线的中垂线,C为A、B两点连线的中点,将一正电荷q3由C点沿着中垂线移至无穷远处的过程中,下列结论正确的有( )
 在真空中有两个等量的正电荷q1和q2,分别固定于A、B两点,DC为AB连线的中垂线,C为A、B两点连线的中点,将一正电荷q3由C点沿着中垂线移至无穷远处的过程中,下列结论正确的有( )
在真空中有两个等量的正电荷q1和q2,分别固定于A、B两点,DC为AB连线的中垂线,C为A、B两点连线的中点,将一正电荷q3由C点沿着中垂线移至无穷远处的过程中,下列结论正确的有( )| A. | 电势能逐渐减小 | B. | 电势能逐渐增大 | ||
| C. | q3受到的电场力逐渐减小 | D. | q3受到的电场力逐渐增大 |