题目内容
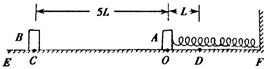
如图所示，EF为水平地面，O点左侧是粗糙的，右侧是光滑的，一轻质弹簧右端固定在墙壁上，左端与静止在O点、质量为m的小物块A连接，弹簧处于原长状态．质量为2m的物块B在大小为F的水平恒力作用下由C处从静止开始向右运动，已知物块B与地面EO段间的滑动摩擦力大小为
，物块B运动到O点与物块A相碰并一起向右运动（设碰撞时间极短），运动到D点时撤去外力F．物块B和物块A可视为质点．已知CD=5L，OD=L．求：
（1）撤去外力后弹簧的最大弹性势能?
（2）物块B从O点开始向左运动直到静
止所用的时间是多少?
（1）
；（2）
解析:
（1）设B与A碰撞前速度为v0，由动能定理，得
，则
B与A在O点碰撞，设碰后共同速度为v1，
由动量守恒得
碰后B和A一起运动，运动到D点时撤去外力F后，当它们的共同速度减小为零时，弹簧的弹性势能最大，设为Epm，则由能量守恒得
（2）设A、B一起向左运动回到O点的速度为v2，由机械能守恒得
经过O点后，B和A分离，B在滑动摩擦力的作用下做匀减速直线运动，设运动时间为t，由动量定理得
，则
．
练习册系列答案
相关题目
如图所示，EF为水平地面，O点左侧是粗糙的、右侧是光滑的．一轻质弹簧右端与墙壁固定，左侧与静止在O点质量为m的小物块A连接，弹簧处于原长状态．质量为4m的物块B在大小为F的水平恒力作用下由C处从静止开始向右运动，已知物块B与地面EO段间的滑动摩擦力大小为
，物块B运动到O点与物块A相碰并一起向右运动（设碰撞时间极短），运动到D点时撤去外力F.已知CO=4s，OD=s.求撤去外力后：
，物块B运动到O点与物块A相碰并一起向右运动（设碰撞时间极短），运动到D点时撤去外力F.已知CO=4s，OD=s.求撤去外力后：
，物块B运动到O点与物块A相碰并一起向右运动（设碰撞时间极短），A、B虽接触而不粘连，当运动到D点时撤去外力F。已知CO长度为4S，OD长度为S，整个过程中
弹簧都在其弹性限度内。求撤去外力后：