题目内容
小球从斜面的顶端以初速度v0=2m/s,加速度a=2m/s2沿斜面向下匀加速滑行,经t=4s到达斜面底端,求:
(1)小球到达斜面底端的速度大小
(2)斜面的长度
(3)小球平均速度大小.
(1)小球到达斜面底端的速度大小
(2)斜面的长度
(3)小球平均速度大小.
分析:(1)根据匀变速直线运动的速度时间公式求出小球到达底端时的速度大小.
(2)根据匀变速直线运动的位移时间公式求出斜面的长度.
(3)根据平均速度的定义式求出小球的平均速度的大小.
(2)根据匀变速直线运动的位移时间公式求出斜面的长度.
(3)根据平均速度的定义式求出小球的平均速度的大小.
解答:解:(1)根据速度时间公式得,v=v0+at=2+2×4m/s=10m/s.
(2)根据位移时间公式得,x=v0t+
at2=2×4+
×2×16m=24m.
(3)小球的平均速度的大小
=
=
m/s=6m/s.
答:(1)小球到达底端时的速度大小为10m/s.
(2)斜面的长度为24m.
(3)小球的平均速度大小为6m/s.
(2)根据位移时间公式得,x=v0t+
| 1 |
| 2 |
| 1 |
| 2 |
(3)小球的平均速度的大小
. |
| v |
| x |
| t |
| 24 |
| 4 |
答:(1)小球到达底端时的速度大小为10m/s.
(2)斜面的长度为24m.
(3)小球的平均速度大小为6m/s.
点评:解决本题的关键掌握匀变速直线运动的运动学公式,并能灵活运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
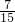 ,求:
,求: