题目内容
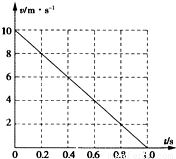一质量m=0.5kg的滑块以一定的初速度冲上一倾角θ=37°足够长的斜面，某同学利用传感器测出了滑块冲上斜面过程中多个时刻的瞬时速度，并用计算机做出了小物块上滑过程的vt图象，如图所示．（最大静摩擦力等于滑动摩擦力，取sin37°=0.6，cos37°=0.8，g=10m/s2）求：（1）滑块与斜面间的动摩擦因数
（2）判断滑块最后能否返回斜面底端？若能返回，求出返回斜面底端时的速度大小；若不能返回，求出滑块停在什么位置．
【答案】分析：（1）先用v-t图象求得滑块的加速度，然后根据牛顿第二定律求得合力，再受力分析，求解出支持力和滑动摩擦力，最后求解动摩擦因素；
（2）通过比较重力的下滑分量和最大静摩擦力的大小判断物体能否下滑，再结合牛顿第二定律和运动学规律计算求未知量．
解答：解：（1）由图象可知，滑块的加速度a=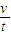
=
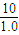m/s2=10 m/s2
滑块冲上斜面过程中根据牛顿第二定律，有mgsinθ+μmgcosθ=ma
代入数据解得μ=0.5
即滑块与斜面间的动摩擦因数为0.5．
（2）由于μ＜tan37°，故滑块速度减小到零时，重力的下滑分力大于最大静摩擦力，即mgsinθ＞μmgcosθ，能再下滑．
由匀变速直线运动的规律，滑块向上运动的位移s=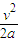
=5 m
滑块下滑过程中根据牛顿第二定律，有mgsinθ-μmgcosθ=ma2，解得a2=2 m/s2
由匀变速直线运动的规律，滑块返回底端的速度v=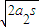
=
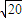m/s
故滑块最后能返回斜面底端；返回 斜面底端时的速度大小为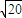
m/s．
点评：本题关键对物体受力分析后，通过正交分解法求出合力，根据牛顿第二定律求得加速度，然后根据运动学公式求解未知量．
（2）通过比较重力的下滑分量和最大静摩擦力的大小判断物体能否下滑，再结合牛顿第二定律和运动学规律计算求未知量．
解答：解：（1）由图象可知，滑块的加速度a=
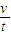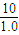=m/s2=10 m/s2滑块冲上斜面过程中根据牛顿第二定律，有mgsinθ+μmgcosθ=ma
代入数据解得μ=0.5
即滑块与斜面间的动摩擦因数为0.5．
（2）由于μ＜tan37°，故滑块速度减小到零时，重力的下滑分力大于最大静摩擦力，即mgsinθ＞μmgcosθ，能再下滑．
由匀变速直线运动的规律，滑块向上运动的位移s=
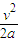=5 m滑块下滑过程中根据牛顿第二定律，有mgsinθ-μmgcosθ=ma2，解得a2=2 m/s2
由匀变速直线运动的规律，滑块返回底端的速度v=
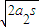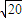=m/s故滑块最后能返回斜面底端；返回 斜面底端时的速度大小为
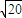m/s．点评：本题关键对物体受力分析后，通过正交分解法求出合力，根据牛顿第二定律求得加速度，然后根据运动学公式求解未知量．
练习册系列答案
阅读快车系列答案
相关题目
一质量m=0.5kg的滑块以一定的初速度冲上一倾角为30°足够长的斜面，某同学利用DIS实验系统测出了滑块冲上斜面过程中多个时刻的瞬时速度，如图所示为通过计算机绘制出的滑块上滑过程的v-t图．求：（g=10m/s2）
如图所示，一对平行光滑轨道放置在水平面上，两轨道相距L=1m，两轨道用R=2Ω的电阻连接，有一质量m=0.5kg的导体杆静止地放在轨道上，与两轨道垂直，杆及轨道的电阻皆可忽略不计，整个装置处于磁感应强度B=2T的匀强磁场中，磁场方向垂直轨道平面向上．现用水平拉力F沿水平方向拉动导体杆，则：
一质量m=0.5kg的滑块以一定的初速度冲上一倾角θ=37°足够长的斜面，已知滑块上滑过程中的v-t图象如图所示．取sin37°=0.6．cos37°=0.8，g=10m/s2，求：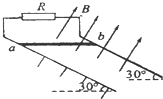
光滑的平行金属导轨长L=2m，两导轨间距d=0.5m，轨道平面与水平面的夹角 θ=30°，导轨上端接一阻值为R=0.6Ω的电阻，轨道所在空间有垂直轨道平面向上的匀强磁场，磁场的磁感应强度B=1T，如图所示．有一质量m=0.5kg、电阻r=0.4Ω的金属棒曲，放在导轨最上端，其余部分点阻不计．当棒ab从轨道最上端由静止开始下滑到底端脱离轨道时，电阻R上产生的热量Q1=0.6J，取g=10m/s2，试求：
（2013?南通二模）如图所示，光滑平行的长金属导轨固定在水平面上，相距L=1m，左端连接R=2Ω电阻，一质量m=0.5kg、电阻r=1Ω的导体棒MN垂直放置在两平行金属导轨上，彼此电接触良好，导轨的电阻不计．在两导轨间有这样的磁场：0≤x≤0.5m区间，磁场方向竖直向下，磁感应强度B大小随x变化关系是