题目内容
如图所示，传送带长为l，运动速率为v0，今在其左端静止地放上一个木块，设木块与传送带之间滑动摩擦系数为μ，放上木块后传送带不受影响．问木块从左端运动到右端需要多少时间？
答案：
解析：
提示：
解析：
|
木块从静止到跟传送带有共同速度总有一个加速过程，在这个过程中，木块的速率一定小于传送带的速率，所以会产生打滑现象．木块所受摩擦力为μmg，加速度为a＝μg，当木块加速到跟传送带速率相同时才一起做匀速运动．木块做加速运动的时间t1＝v0/μg，做加速运动的位移为x1＝v02/2μg．木块做匀速运动的时间为t2＝(l－v02/2μg)/v0，所以，木块从左端运动至右端的总时间为t＝t1＋t2＝l/v0＋v0/2μg． |
提示：
|
有同学在解决本题时认为当静摩擦系数较大的情况下，放在传送带上的木块可不打滑立即跟着传送带做匀速运动，所以t＝l/v0．这种错解的原因是没有仔细分析物理过程，忽略了木块从静止到跟传送带有共同速度总有一个加速过程．由上述分析的前提条件是：木块最终能与传送带一起运动．若摩擦系数很小，传送带长度l很短，木块最终仍未能跟着传送带运动，即l＜v02/2μg，则t2小于零，无意义；t1＝v0/μg也不能成立．这时木块始终处于加速运动状态l＝ 在解决力和运动的问题时往往求一些物体间的作用力，应注意题目所求的力是谁对谁的力，有时可用牛顿第三定律． |
μgt2，木块从左端运动到右端的时间为t＝
．
练习册系列答案
培优口算题卡系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
如图所示，一块长为L、质量m的扁平均匀规则木板通过装有传送带的光滑斜面输送，斜面与传送带靠在一起并与传送带上表面连成一直线，与水平方向夹角为θ，传送带以较大的恒定速率转动，传送方向向上，木板与传送带之间动摩擦因数为常数，已知木板放在斜面或者传送带上任意位置时，支持力均匀作用在木板底部，将木板静止放在传送带和光滑斜面之间某一位置，位于传送带部位的长度设为x，当
如图所示，一块长为L、质量m的扁平均匀规则木板通过装有传送带的光滑斜面输送．斜面与传送带靠在一起连成一直线，与水平方向夹角θ，传送带以较大的恒定速率转动，传送方向向上，木板与传送带之间动摩擦因数为常数．已知木板处在斜面或者传送带上任意位置时，支持力都均匀作用在木板底部．将木板静止放在传送带和光滑斜面之间某一位置，位于传送带部位的长度设为x，当x=
如图所示，传送带长6m，与水平方向的夹角θ=37°，以5m/s的速度向上运动．一个质量为2kg的物块（可视为质点），沿平行于传送带方向以10m/s的速度滑上传送带，已知物块与传送带之间的动摩擦因数μ=0.5．求：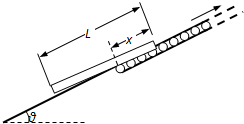
如图所示，一块长为L、质量m的扁平均匀规则木板通过装有传送带的光滑斜面输送．斜面与传送带靠在一起连成一直线，与水平方向夹角θ，传送带以较大的恒定速率转动，传送方向向上，木板与传送带之间动摩擦因数为常数．已知木板放在斜面或者传送带上任意位置时，支持力均匀作用在木板底部．将木板静止放在传送带和光滑斜面之间某一位置，位于传送带部位的长度设为x，当x=L/4时，木板能保持静止．