题目内容
 如图所示,一块长为L、质量m的扁平均匀规则木板通过装有传送带的光滑斜面输送.斜面与传送带靠在一起连成一直线,与水平方向夹角θ,传送带以较大的恒定速率转动,传送方向向上,木板与传送带之间动摩擦因数为常数.已知木板处在斜面或者传送带上任意位置时,支持力都均匀作用在木板底部.将木板静止放在传送带和光滑斜面之间某一位置,位于传送带部位的长度设为x,当x=
如图所示,一块长为L、质量m的扁平均匀规则木板通过装有传送带的光滑斜面输送.斜面与传送带靠在一起连成一直线,与水平方向夹角θ,传送带以较大的恒定速率转动,传送方向向上,木板与传送带之间动摩擦因数为常数.已知木板处在斜面或者传送带上任意位置时,支持力都均匀作用在木板底部.将木板静止放在传送带和光滑斜面之间某一位置,位于传送带部位的长度设为x,当x=| L |
| 4 |
(1)将木板静止放在x=
| L |
| 2 |
(2)木板从x=
| L |
| 2 |
(3)在(2)的过程中,木块的机械能增加量设为△E,传送带消耗的电能设为W,不计电路中产生的电热,比较△E和W的大小关系,用文字说明理由.
分析:(1)根据木板静止,得出此时摩擦力的大小,当x加倍时,正压力加倍,则摩擦力加倍,结合牛顿第二定律求出木板的加速度大小.
(2)根据摩擦力f与x的图象求出摩擦力做功的大小,结合动能定理求出木板的速度大小.
(3)根据能量守恒定律比较△E和W的大小关系
(2)根据摩擦力f与x的图象求出摩擦力做功的大小,结合动能定理求出木板的速度大小.
(3)根据能量守恒定律比较△E和W的大小关系
解答:解:(1)x=
时,摩擦力为:f1=mgsinθ
x=
时,摩擦力加倍,为:f1=2mgsinθ
由牛顿运动定律得:a=
=gsinθ
(2)作出摩擦力与x的图象,可知摩擦力做功:W=
mgLsinθ
由动能定理有:W-
mgLsinθ=
mv2
得:v=
(3)△E小于W
因为传送带与木板之间有滑动摩擦,电能有一部分转为了内能.
答:(1)木板释放瞬间加速度为gsinθ.
(2)木板的速度为v=
.
(3))△E小于W因为传送带与木板之间有滑动摩擦,电能有一部分转为了内能.
| L |
| 4 |

x=
| L |
| 2 |
由牛顿运动定律得:a=
| f2-mgsinθ |
| m |
(2)作出摩擦力与x的图象,可知摩擦力做功:W=
| 3 |
| 2 |
由动能定理有:W-
| 1 |
| 2 |
| 1 |
| 2 |
得:v=
| 2gLsinθ |
(3)△E小于W
因为传送带与木板之间有滑动摩擦,电能有一部分转为了内能.
答:(1)木板释放瞬间加速度为gsinθ.
(2)木板的速度为v=
| 2gLsinθ |
(3))△E小于W因为传送带与木板之间有滑动摩擦,电能有一部分转为了内能.
点评:解决本题的关键知道摩擦力与x关系图线围成的面积表示摩擦力做功的大小,结合牛顿第二定律和动能定理进行求解.

练习册系列答案
相关题目
 如图所示,一块长为L、质量m的扁平均匀规则木板通过装有传送带的光滑斜面输送,斜面与传送带靠在一起并与传送带上表面连成一直线,与水平方向夹角为θ,传送带以较大的恒定速率转动,传送方向向上,木板与传送带之间动摩擦因数为常数,已知木板放在斜面或者传送带上任意位置时,支持力均匀作用在木板底部,将木板静止放在传送带和光滑斜面之间某一位置,位于传送带部位的长度设为x,当
如图所示,一块长为L、质量m的扁平均匀规则木板通过装有传送带的光滑斜面输送,斜面与传送带靠在一起并与传送带上表面连成一直线,与水平方向夹角为θ,传送带以较大的恒定速率转动,传送方向向上,木板与传送带之间动摩擦因数为常数,已知木板放在斜面或者传送带上任意位置时,支持力均匀作用在木板底部,将木板静止放在传送带和光滑斜面之间某一位置,位于传送带部位的长度设为x,当 (2009?上海二模)如图所示,一块长为L、质量m的扁平均匀规则木板通过装有传送带的光滑斜面输送.斜面与传送带靠在一起连成一直线,与水平方向夹角θ,传送带以较大的恒定速率转动,传送方向向上,木板与传送带之间动摩擦因数为常数.已知木板放在斜面或者传送带上任意位置时,支持力均匀作用在木板底部.将木板静止放在传送带和光滑斜面之间某一位置,位于传送带部位的长度设为x,当x=L/4时,木板能保持静止.
(2009?上海二模)如图所示,一块长为L、质量m的扁平均匀规则木板通过装有传送带的光滑斜面输送.斜面与传送带靠在一起连成一直线,与水平方向夹角θ,传送带以较大的恒定速率转动,传送方向向上,木板与传送带之间动摩擦因数为常数.已知木板放在斜面或者传送带上任意位置时,支持力均匀作用在木板底部.将木板静止放在传送带和光滑斜面之间某一位置,位于传送带部位的长度设为x,当x=L/4时,木板能保持静止.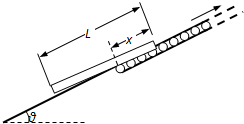 如图所示,一块长为L、质量m的扁平均匀规则木板通过装有传送带的光滑斜面输送.斜面与传送带靠在一起连成一直线,与水平方向夹角θ,传送带以较大的恒定速率转动,传送方向向上,木板与传送带之间动摩擦因数为常数.已知木板放在斜面或者传送带上任意位置时,支持力均匀作用在木板底部.将木板静止放在传送带和光滑斜面之间某一位置,位于传送带部位的长度设为x,当x=L/4时,木板能保持静止.
如图所示,一块长为L、质量m的扁平均匀规则木板通过装有传送带的光滑斜面输送.斜面与传送带靠在一起连成一直线,与水平方向夹角θ,传送带以较大的恒定速率转动,传送方向向上,木板与传送带之间动摩擦因数为常数.已知木板放在斜面或者传送带上任意位置时,支持力均匀作用在木板底部.将木板静止放在传送带和光滑斜面之间某一位置,位于传送带部位的长度设为x,当x=L/4时,木板能保持静止. ,传送带以较大的恒定速率转动,传送方向向上,木板与传送带之间动摩擦因数为常数,已知木板放在斜面或者传送带上任意位置时,支持力均匀作用在木板底部,将木板静止放在传送带和光滑斜面之间某一位置,位于传送带部位的长度设为x,当
,传送带以较大的恒定速率转动,传送方向向上,木板与传送带之间动摩擦因数为常数,已知木板放在斜面或者传送带上任意位置时,支持力均匀作用在木板底部,将木板静止放在传送带和光滑斜面之间某一位置,位于传送带部位的长度设为x,当 时,木板能保持静止。
时,木板能保持静止。 的位置静止释放,当移动到x=L的位置时,木板的速度多大?
的位置静止释放,当移动到x=L的位置时,木板的速度多大?