题目内容
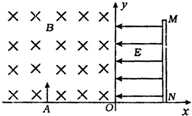 如图所示,坐标平面的第Ⅰ象限内存在大小为E、方向水平向左的匀强电场,足够长的挡板MN垂直x轴放置且距离点O为d,第Ⅱ象限内存在垂直于纸面向里的匀强磁场,磁感应强度为B.一质量为m,带电量为一q的粒子(重力忽略不计)若自距原点O为L的A点以一定的速度垂直x轴进入磁场,则粒子恰好到达O点而不进入电场.现将该种粒子两个仍从A点但以不同方向先后射入磁场,但初速度大小变为原来的4倍,为使粒子进入电场后能同时垂直到达挡板MN上被吸收,求:
如图所示,坐标平面的第Ⅰ象限内存在大小为E、方向水平向左的匀强电场,足够长的挡板MN垂直x轴放置且距离点O为d,第Ⅱ象限内存在垂直于纸面向里的匀强磁场,磁感应强度为B.一质量为m,带电量为一q的粒子(重力忽略不计)若自距原点O为L的A点以一定的速度垂直x轴进入磁场,则粒子恰好到达O点而不进入电场.现将该种粒子两个仍从A点但以不同方向先后射入磁场,但初速度大小变为原来的4倍,为使粒子进入电场后能同时垂直到达挡板MN上被吸收,求:(1)这两个粒子从A点射入磁场的时间间隔.
(2)粒子打到挡板MN上时的速度大小.
分析:画出轨迹由几何关系确定粒子的半径大小,然后根据半径公式求出粒子的速度,然后求而出当速度加倍后的半径
解答:解:(1)粒子在磁场中作圆周运动半径为r,速度为v0,由牛顿第二定律知:
qv0B=m
所以圆周运动的半径为r=
由几何关系知:r=
得初速度大小为v0=
设粒子初速度为原来的4倍时半径为r1,速度为v1,由牛顿第二定律知:
qv1B=m
v1=4v0
解得:r1=2L
v1=
为使粒子进入电场后能垂直到达挡板MN上,粒子必须平行x轴进入电场,圆心O在y轴上,设速度方向与x轴正方向夹角为θ,由几何关系知:
sinθ=
=
=
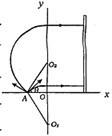
所以θ=30°或θ=150°
粒子在磁场中运动时间分别为t1=
T=
t2=
T=
两粒子射入的时间间隔△t=t2-t1=
(2)设粒子到达挡板速度为v2,由动能定理知:
qEd=
mv22-
mv12
解得:v2=
答:(1)这两个粒子从A点射入磁场的时间间隔=
.
(2)粒子打到挡板MN上时的速度大小为
.
qv0B=m
| v02 |
| r |
所以圆周运动的半径为r=
| mv0 |
| qB |
由几何关系知:r=
| l |
| 2 |
得初速度大小为v0=
| Bql |
| 2m |
设粒子初速度为原来的4倍时半径为r1,速度为v1,由牛顿第二定律知:
qv1B=m
| v12 |
| r1 |
v1=4v0
解得:r1=2L
v1=
| 2qBL |
| m |
为使粒子进入电场后能垂直到达挡板MN上,粒子必须平行x轴进入电场,圆心O在y轴上,设速度方向与x轴正方向夹角为θ,由几何关系知:
sinθ=
| OA |
| O1A |
| L |
| 2L |
| 1 |
| 2 |

所以θ=30°或θ=150°
粒子在磁场中运动时间分别为t1=
| 30° |
| 360° |
| πm |
| 6Bq |
t2=
| 150° |
| 360° |
| 5πm |
| 6Bq |
两粒子射入的时间间隔△t=t2-t1=
| 2πm |
| 3Bq |
(2)设粒子到达挡板速度为v2,由动能定理知:
qEd=
| 1 |
| 2 |
| 1 |
| 2 |
解得:v2=
|
答:(1)这两个粒子从A点射入磁场的时间间隔=
| 2πm |
| 3Bq |
(2)粒子打到挡板MN上时的速度大小为
|
点评:本题考查了带电粒子在组合场中的运动,画出轨迹分阶段处理是关键,带电粒子在电场中加速的情况通常由动能定理解决比较简单.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
 (2012?丹东模拟)如图所示,坐标平面的第I象限内存在大小为E、方向水平向左的匀强电场,足够长的挡板MN垂直x轴放置且距离点O为d,第II象限内存在垂直于纸面向里的匀强磁场,磁感应强度为B.一质量为m,带电量为-q的粒子(重力忽略不计)若自距原点O为L的A点以一定的速度垂直x轴进入磁场,则粒子恰好到达O点而不进入电场.现该粒子仍从A点进入磁场,但初速度大小为原来的4倍,为使粒子进入电场后能垂直到达挡板MN上,求:
(2012?丹东模拟)如图所示,坐标平面的第I象限内存在大小为E、方向水平向左的匀强电场,足够长的挡板MN垂直x轴放置且距离点O为d,第II象限内存在垂直于纸面向里的匀强磁场,磁感应强度为B.一质量为m,带电量为-q的粒子(重力忽略不计)若自距原点O为L的A点以一定的速度垂直x轴进入磁场,则粒子恰好到达O点而不进入电场.现该粒子仍从A点进入磁场,但初速度大小为原来的4倍,为使粒子进入电场后能垂直到达挡板MN上,求:
