题目内容
10.假设航天员站在一星球表面上的某高处,沿水平方向抛出一个小球,经过时间t小球落到星球表面,测得抛出点与落点之间的距离为L1,若抛出时的速度增大到2倍,则抛出点与落点之间的距离为L2,已知星球的半径为R,引力常量为G,求该星球的质量m′.分析 根据平抛运动的规律,知初速度增大到2倍,则水平位移也增大2倍,结合几何关系求出小球落地的高度,通过平抛运动竖直方向上的运动规律求出重力加速度的大小,结合万有引力等于重力求出月球的质量M.
解答 解:设抛出点的高度为h,第一次平抛运动时:L12=h2+(vt)2…①
若抛出的初速度为2倍时,因此有:L22=h2+(2vt)2…②
设该星球表面的重力加速度为g,则$h=\frac{1}{2}g{t}_{\;}^{2}$…③
联立①②③得:${t}^{2}=\frac{{L}_{2}^{2}-{L}_{1}^{2}}{3{v}^{2}}$
代入①得:g=$\sqrt{\frac{8{L}_{1}^{2}-4{L}_{2}^{2}}{3t}}$
根据星球表面物体重力等于万有引力为:$mg=\frac{Gmm′}{{R}^{2}}$
解得:m′=$\frac{g{R}^{2}}{G}$=$\frac{{R}^{2}}{G}•\sqrt{\frac{8{L}_{1}^{2}-4{L}_{2}^{2}}{3t}}$
答:该星球质量为$\frac{{R}^{2}}{G}•\sqrt{\frac{8{L}_{1}^{2}-4{L}_{2}^{2}}{3t}}$.
点评 本题综合考查了平抛运动和万有引力的综合,知道平抛运动在水平方向上和竖直方向上的运动规律,以及掌握万有引力等于重力这一理论,并能灵活运用.

练习册系列答案
相关题目
3. 如图所示,一质量为m的滑块沿光滑的水平面以速度v0运动.遇到竖直的墙壁被反弹回来,返回的速度变为$\frac{1}{2}$v0,则以下说法正确的是( )
如图所示,一质量为m的滑块沿光滑的水平面以速度v0运动.遇到竖直的墙壁被反弹回来,返回的速度变为$\frac{1}{2}$v0,则以下说法正确的是( )
 如图所示,一质量为m的滑块沿光滑的水平面以速度v0运动.遇到竖直的墙壁被反弹回来,返回的速度变为$\frac{1}{2}$v0,则以下说法正确的是( )
如图所示,一质量为m的滑块沿光滑的水平面以速度v0运动.遇到竖直的墙壁被反弹回来,返回的速度变为$\frac{1}{2}$v0,则以下说法正确的是( )| A. | 滑块的动量改变量的大小为$\frac{1}{2}$mv0 | |
| B. | 滑块的动量改变量的大小为$\frac{3}{2}$mv0 | |
| C. | 滑块的动量改变量的方向与v0的方向相同 | |
| D. | 重力对滑块的冲量为零 |
5.下列说法正确的是( )
| A. | 气体如果失去了容器的约束就会散开,这是因为气体分子之间存在斥力的缘故 | |
| B. | 当分子间的引力和斥力平衡时,分子势能最小 | |
| C. | 一定量100℃的水变成100℃的水蒸气,其分子之间的势能增加 | |
| D. | 一定量的气体,在压强不变时,分子每秒对器壁单位面积平均碰撞次数随着温度降低而减少 |
15.一定质量的理想气体,经过一个压缩过程后,体积减小为原来的一半,这个过程可以是等温的、绝热的或等压的过程.在这三个过程中( )
| A. | 绝热过程做功最多 | B. | 等热过程做功最多 | ||
| C. | 等压过程内能减少 | D. | 等温过程对外放热 |
9.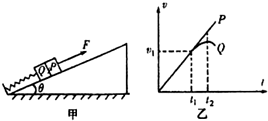 如图甲所示,平行于斜面的轻弹簧,劲度系数为k,一端固定在倾角为θ的斜面底端,另一端与Q物块连接,P、Q质量均为m,斜面光滑且固定在水平面上,初始时物块均静止.现用平行于斜面向上的力F拉物块P,使P做加速度为a的匀加速运动,两个物块在开始一段时间内的v-t图象如图乙所示(重力加速度为g),则( )
如图甲所示,平行于斜面的轻弹簧,劲度系数为k,一端固定在倾角为θ的斜面底端,另一端与Q物块连接,P、Q质量均为m,斜面光滑且固定在水平面上,初始时物块均静止.现用平行于斜面向上的力F拉物块P,使P做加速度为a的匀加速运动,两个物块在开始一段时间内的v-t图象如图乙所示(重力加速度为g),则( )
 如图甲所示,平行于斜面的轻弹簧,劲度系数为k,一端固定在倾角为θ的斜面底端,另一端与Q物块连接,P、Q质量均为m,斜面光滑且固定在水平面上,初始时物块均静止.现用平行于斜面向上的力F拉物块P,使P做加速度为a的匀加速运动,两个物块在开始一段时间内的v-t图象如图乙所示(重力加速度为g),则( )
如图甲所示,平行于斜面的轻弹簧,劲度系数为k,一端固定在倾角为θ的斜面底端,另一端与Q物块连接,P、Q质量均为m,斜面光滑且固定在水平面上,初始时物块均静止.现用平行于斜面向上的力F拉物块P,使P做加速度为a的匀加速运动,两个物块在开始一段时间内的v-t图象如图乙所示(重力加速度为g),则( )| A. | 施加拉力前,Q给P的力大小为mgsinθ | |
| B. | 施加拉力前,弹簧的形变量为$\frac{2mgsinθ}{k}$ | |
| C. | 到t1时刻,弹簧释放的弹性势能为$\frac{1}{2}$mv12 | |
| D. | t2时刻弹簧恢复到原长,物块Q达到速度最大值 |
 可看作质点的滑块质量为m,置于光滑半球面的顶点A处(半球面固定不动),如图所示.当它由静止开始下滑到半球面上B点时(未脱离半球面),它的加速度的大小为$g\sqrt{4{(1-cosθ)}^{2}+{(sinθ)}^{2}}$.
可看作质点的滑块质量为m,置于光滑半球面的顶点A处(半球面固定不动),如图所示.当它由静止开始下滑到半球面上B点时(未脱离半球面),它的加速度的大小为$g\sqrt{4{(1-cosθ)}^{2}+{(sinθ)}^{2}}$. 如图所示:电源的电动势为E=9V内阻为1Ω,电阻R1=5Ω、R2=3Ω,电流表理想电表.求:
如图所示:电源的电动势为E=9V内阻为1Ω,电阻R1=5Ω、R2=3Ω,电流表理想电表.求:
 “霾”主要指原因不明的因大量烟、尘等微粒悬浮而形成的浑浊现象.根据目前的认识,机动车尾气排放、煤炭燃烧和工业生产的燃烧过程中排放的二氧化硫和氮氧化物等是产生霾的主要来源.它会对人的呼吸系统、神经系统等产生影响.将火车由燃烧汽油、柴油等改为使用电力,是从源头减少“霾”的重要措施.高铁列车采用动力分散的电力机车驱动方式.国家电网将220kV高压电送至高铁牵引站,经牵引站变压后送达接触网.铁路沿线上方悬挂着的金属线就是接触网.接触网额定电压为25kV.车顶伸出的“长辫子”般的受电弓与接触网滑动接触获得电能而牵引列车运行.假设列车由18节车厢组成,除第1、18节两车厢为无动力车厢外,其余16节车厢均装备动力系统,各动力车厢产生的动力相同,每节车厢(含乘客行李等)的平均质量均为10吨.假设运动时每节车厢所受的阻力恒为车重的$\frac{1}{36}$倍,该列车匀加速启动时,能在800s内将速度提升到360公里每小时,此后列车保持恒定功率,列车达到最大速度后匀速运动.(g取10m/s2.)求:
“霾”主要指原因不明的因大量烟、尘等微粒悬浮而形成的浑浊现象.根据目前的认识,机动车尾气排放、煤炭燃烧和工业生产的燃烧过程中排放的二氧化硫和氮氧化物等是产生霾的主要来源.它会对人的呼吸系统、神经系统等产生影响.将火车由燃烧汽油、柴油等改为使用电力,是从源头减少“霾”的重要措施.高铁列车采用动力分散的电力机车驱动方式.国家电网将220kV高压电送至高铁牵引站,经牵引站变压后送达接触网.铁路沿线上方悬挂着的金属线就是接触网.接触网额定电压为25kV.车顶伸出的“长辫子”般的受电弓与接触网滑动接触获得电能而牵引列车运行.假设列车由18节车厢组成,除第1、18节两车厢为无动力车厢外,其余16节车厢均装备动力系统,各动力车厢产生的动力相同,每节车厢(含乘客行李等)的平均质量均为10吨.假设运动时每节车厢所受的阻力恒为车重的$\frac{1}{36}$倍,该列车匀加速启动时,能在800s内将速度提升到360公里每小时,此后列车保持恒定功率,列车达到最大速度后匀速运动.(g取10m/s2.)求: