题目内容
3. 如图所示,正方形单匝均匀线框abcd边长L=0.4m,每边电阻相等,总电阻R=0.5Ω.一根足够长的绝缘轻质细线跨过两个轻质光滑定滑轮,一端连接正方形线框,另一端连接绝缘物体P,物体P放在一个光滑的足够长的固定斜面上,斜面倾角θ=30°,斜面上方的细线与斜面平行.在正方形线框正下方有一有界的匀强磁场,上边界I和下边界Ⅱ都水平,两边界之间距离也是L=0.4m.磁场方向水平且垂直纸面向里,磁感应强度大小B=0.5T.现让正方形线框的cd边距上边界I的正上方高度h=0.9m的位置由静止释放,且线框在运动过程中始终与磁场垂直,cd边始终保持水平,物体P始终在斜面上运动,线框刚好能以v=3m/s的速度进入并匀速通过磁场区域.释放前细线绷紧,重力加速度g=10m/s2,不计空气阻力.
如图所示,正方形单匝均匀线框abcd边长L=0.4m,每边电阻相等,总电阻R=0.5Ω.一根足够长的绝缘轻质细线跨过两个轻质光滑定滑轮,一端连接正方形线框,另一端连接绝缘物体P,物体P放在一个光滑的足够长的固定斜面上,斜面倾角θ=30°,斜面上方的细线与斜面平行.在正方形线框正下方有一有界的匀强磁场,上边界I和下边界Ⅱ都水平,两边界之间距离也是L=0.4m.磁场方向水平且垂直纸面向里,磁感应强度大小B=0.5T.现让正方形线框的cd边距上边界I的正上方高度h=0.9m的位置由静止释放,且线框在运动过程中始终与磁场垂直,cd边始终保持水平,物体P始终在斜面上运动,线框刚好能以v=3m/s的速度进入并匀速通过磁场区域.释放前细线绷紧,重力加速度g=10m/s2,不计空气阻力.(1)线框的cd边在匀强磁场中运动的过程中,c、d间的电压是多大?
(2)线框的质量m1和物体P的质量m2分别是多大?
分析 (1)线框进入磁场时,cd边切割磁感线运动,由E=BLv可求得电动势,由闭合电路欧姆定律可求得感应电流,再求c、d间的电压Ucd.
(2)线框刚好能进入并匀速通过磁场区域,合力为零,由平衡条件和能量守恒定律结合可求得线框的质量m1和物体P的质量m2.
解答 解:(1)正方形线框匀速通过匀强磁场区域的过程中,设cd边上的感应电动势为E,线框中的电流强度为I,c、d间的电压为Ucd,则有:
E=BLv
由欧姆定律得:I=$\frac{E}{R}$
Ucd=I•$\frac{3}{4}$R
解得:Ucd=0.45V
(2)正方形线框匀速通过磁场区域的过程中,设受到的安培力为F,细线上的张力为T,则有:
F=BIL
对物体P受力分析有:T=m2gsinθ
对线框分析受力有:m1g=T+F
正方形线框在进入磁场之前的运动过程中,根据能量守恒,则有:
m1gh-m2ghsinθ=$\frac{1}{2}$(m1+m2)v2;
解得:m1=0.032kg,m2=0.016kg
答:(1)线框的cd边在匀强磁场中运动的过程中,c、d间的电压是0.45V.
(2)线框的质量m1和物体P的质量m2分别是0.032kg和0.016kg.
点评 本题考查了电磁感应与力学知识的综合,要知道物体P和线框都做匀速运动时,合力均为零,计算出安培力的大小是关键.要注意c、d间的电压相当于路端电压,不是电源的内电压.

练习册系列答案
相关题目
18.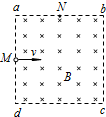 如图所示,正方形区域abcd中有一匀强磁场,磁感应强度B的方向垂直于纸面向里,一个氢核从ad边的中点M沿着纸面垂直于ad边,以一定的速度射入磁场,正好从ab边中点N射出,现将磁场的磁感应强度变为原来的一半,其他条件不变,则这个氢核射出磁场的位置是( )
如图所示,正方形区域abcd中有一匀强磁场,磁感应强度B的方向垂直于纸面向里,一个氢核从ad边的中点M沿着纸面垂直于ad边,以一定的速度射入磁场,正好从ab边中点N射出,现将磁场的磁感应强度变为原来的一半,其他条件不变,则这个氢核射出磁场的位置是( )
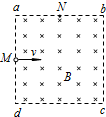 如图所示,正方形区域abcd中有一匀强磁场,磁感应强度B的方向垂直于纸面向里,一个氢核从ad边的中点M沿着纸面垂直于ad边,以一定的速度射入磁场,正好从ab边中点N射出,现将磁场的磁感应强度变为原来的一半,其他条件不变,则这个氢核射出磁场的位置是( )
如图所示,正方形区域abcd中有一匀强磁场,磁感应强度B的方向垂直于纸面向里,一个氢核从ad边的中点M沿着纸面垂直于ad边,以一定的速度射入磁场,正好从ab边中点N射出,现将磁场的磁感应强度变为原来的一半,其他条件不变,则这个氢核射出磁场的位置是( )| A. | a点 | B. | b点 | C. | 在N、a之间某点 | D. | 在N、b之间某点 |
8.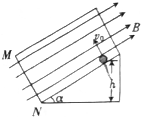 绝缘光滑斜面与水平面成α角,质量为m、带电荷量为-q(q>0)的小球从斜面上的h高度处释放,初速度为v0(v0>0),方向与斜面底边MN平行,如图所示,整个装置处在匀强磁场B中,磁场方向平行斜面向上.如果斜面足够大,且小球能够沿斜面到达底边MN.则下列判断正确的是( )
绝缘光滑斜面与水平面成α角,质量为m、带电荷量为-q(q>0)的小球从斜面上的h高度处释放,初速度为v0(v0>0),方向与斜面底边MN平行,如图所示,整个装置处在匀强磁场B中,磁场方向平行斜面向上.如果斜面足够大,且小球能够沿斜面到达底边MN.则下列判断正确的是( )
 绝缘光滑斜面与水平面成α角,质量为m、带电荷量为-q(q>0)的小球从斜面上的h高度处释放,初速度为v0(v0>0),方向与斜面底边MN平行,如图所示,整个装置处在匀强磁场B中,磁场方向平行斜面向上.如果斜面足够大,且小球能够沿斜面到达底边MN.则下列判断正确的是( )
绝缘光滑斜面与水平面成α角,质量为m、带电荷量为-q(q>0)的小球从斜面上的h高度处释放,初速度为v0(v0>0),方向与斜面底边MN平行,如图所示,整个装置处在匀强磁场B中,磁场方向平行斜面向上.如果斜面足够大,且小球能够沿斜面到达底边MN.则下列判断正确的是( )| A. | 匀强磁场磁感应强度的取值范围为0≤B≤$\frac{mg}{q{v}_{0}}$ | |
| B. | 匀强磁场磁感应强度的取值范围为0≤B≤$\frac{mgcosα}{q{v}_{0}}$ | |
| C. | 小球在斜面做变加速曲线运动 | |
| D. | 小球到达底边MN的时间t=$\sqrt{\frac{2h}{gsi{n}^{2}α}}$ |
15. 如图所示,一平行板电容器的电容为C,两极板M、N间距离为d,所接电源的电动势为E,两板间a、b、c三点的连线构成一等腰直角三角形.三角形的两直角边长均为L,其中ab边与两板平行,以下说法正确的是( )
如图所示,一平行板电容器的电容为C,两极板M、N间距离为d,所接电源的电动势为E,两板间a、b、c三点的连线构成一等腰直角三角形.三角形的两直角边长均为L,其中ab边与两板平行,以下说法正确的是( )
 如图所示,一平行板电容器的电容为C,两极板M、N间距离为d,所接电源的电动势为E,两板间a、b、c三点的连线构成一等腰直角三角形.三角形的两直角边长均为L,其中ab边与两板平行,以下说法正确的是( )
如图所示,一平行板电容器的电容为C,两极板M、N间距离为d,所接电源的电动势为E,两板间a、b、c三点的连线构成一等腰直角三角形.三角形的两直角边长均为L,其中ab边与两板平行,以下说法正确的是( )| A. | 电容器所带电荷量为2CE | |
| B. | 两极板间匀强电场的电场强度大小为$\frac{E}{d}$ | |
| C. | a、c两点间的电势差为$\frac{\sqrt{2}EL}{d}$ | |
| D. | 若增大两板间距离时,a、c两点间电势差不变 |
13.电容器是一种常用的电子元件.下列对电容器认识正确的是( )
| A. | 电容器的电容表示其储存电荷能力 | |
| B. | 电容器的电容与它所带的电量成正比 | |
| C. | 电容器的电容与它两极板间的电压成反比 | |
| D. | 电容的常用单位有μF和pF,1μF=103pF |

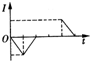
 如图所示,边长为2l的正方形虚线框内有垂直于纸面向里的匀强磁场,一个直角边长为l的等腰直角三角形导线框所在平面与磁场方向垂直,导线框斜边的中线和虚线框的一条对角线恰好共线.从t=0开始,使导线框从图示位置开始以恒定速度沿对角线方向进入磁场,直到整个导线框离开磁场区域.用I表示导线框中的感应电流(逆时针方向为正),则下列表示I-t关系的图象中,正确的是( )
如图所示,边长为2l的正方形虚线框内有垂直于纸面向里的匀强磁场,一个直角边长为l的等腰直角三角形导线框所在平面与磁场方向垂直,导线框斜边的中线和虚线框的一条对角线恰好共线.从t=0开始,使导线框从图示位置开始以恒定速度沿对角线方向进入磁场,直到整个导线框离开磁场区域.用I表示导线框中的感应电流(逆时针方向为正),则下列表示I-t关系的图象中,正确的是( )


 如图所示,在直角坐标系的第Ⅱ象限中,一边长为L的正方形区域内存在磁感应强度大小为B、方向垂直xOy平面向里的匀强磁场,磁场的下边界与x轴重合,右边界与y轴重合,在第Ⅰ、Ⅳ象限x<L区域内存在沿y轴负方向的匀强电场,电场强度大小为E,在x>L区域内存在磁感应强度大小为B′、方向垂直纸面向里的矩形匀强磁场;一质量为m、电荷量为q的带正电的粒子(重力不计)以沿y轴负方向的速度进入第Ⅱ象限的匀强磁场区域,并从坐标原点O处沿x轴正方向射入匀强电场区域;
如图所示,在直角坐标系的第Ⅱ象限中,一边长为L的正方形区域内存在磁感应强度大小为B、方向垂直xOy平面向里的匀强磁场,磁场的下边界与x轴重合,右边界与y轴重合,在第Ⅰ、Ⅳ象限x<L区域内存在沿y轴负方向的匀强电场,电场强度大小为E,在x>L区域内存在磁感应强度大小为B′、方向垂直纸面向里的矩形匀强磁场;一质量为m、电荷量为q的带正电的粒子(重力不计)以沿y轴负方向的速度进入第Ⅱ象限的匀强磁场区域,并从坐标原点O处沿x轴正方向射入匀强电场区域;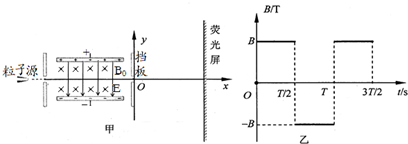 如图甲所示,在坐标系xOy平面内,y轴的左侧有一个速度选择器,其中电场强度为E,磁感应强度为B0.粒子源不断地释放出沿x轴正方向运动,质量均为m、电量均为+q、速度大小不同的粒子.在y轴的右侧有一匀强磁场,磁感应强度大小恒为B,方向垂直于xOy平面,且随时间做周期性变化(不计其产生的电场对粒子的影响),规定垂直xOy平面向里的磁场方向为正,如图乙所示.在离y轴足够远的地方有一个与y轴平行的荧光屏.假设带电粒子在y轴右侧运动的时间达到磁场的一个变化周期之后,失去电荷变为中性粒子.(粒子的重力忽略不计)
如图甲所示,在坐标系xOy平面内,y轴的左侧有一个速度选择器,其中电场强度为E,磁感应强度为B0.粒子源不断地释放出沿x轴正方向运动,质量均为m、电量均为+q、速度大小不同的粒子.在y轴的右侧有一匀强磁场,磁感应强度大小恒为B,方向垂直于xOy平面,且随时间做周期性变化(不计其产生的电场对粒子的影响),规定垂直xOy平面向里的磁场方向为正,如图乙所示.在离y轴足够远的地方有一个与y轴平行的荧光屏.假设带电粒子在y轴右侧运动的时间达到磁场的一个变化周期之后,失去电荷变为中性粒子.(粒子的重力忽略不计)