题目内容
如图所示,一根质量不计的轻弹簧上端固定在天花板上,下端与一质量为m的托盘连接,托盘中有一个质量为M的砝码。当托盘静止时,弹簧的伸长量为L。现将托盘向下拉,弹簧又伸长了 (未超过弹簧的弹性限度),然后使托盘由静止释放,则刚释放托盘时,砝码对托盘的作用力等于
(未超过弹簧的弹性限度),然后使托盘由静止释放,则刚释放托盘时,砝码对托盘的作用力等于

A.
B.
C.
D.
【答案】
A
【解析】
试题分析:当托盘静止时,以托盘和砝码整体为研究对象:当托盘静止时受到平衡力的作用,设弹簧的劲度系数为k,由胡克定律:(m+M)g=kL
① 弹簧又伸长ΔL释放后,由牛顿第二定律:k(L+ΔL)-(m+M)g=(m+M)a ② 以砝码为研究对象:设托盘对砝码的作用力为FN :由牛顿第二定律:FN-Mg=Ma ③
联立以上三式解得:FN= ,由牛顿第三定律:砝码对托盘的作用力为
,由牛顿第三定律:砝码对托盘的作用力为 ,A正确。
,A正确。
考点:本题考查胡克定律、牛顿第二定律、整体隔离法的应用。

练习册系列答案
相关题目
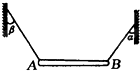 如图所示,一根质量不均匀的木杆,被细绳拉成水平,且∠α>∠β,木杆的重心位置是( )
如图所示,一根质量不均匀的木杆,被细绳拉成水平,且∠α>∠β,木杆的重心位置是( )| A、靠近A端 | B、靠近B端 | C、在AB的中点 | D、无法确定 |
 如图所示,一根质量不计的轻弹簧上端固定在天花板上,下端与一质量为m的托盘连接,托盘中有一个质量为M的砝码.当托盘静止时,弹簧的伸长量为L.现将托盘向下拉,弹簧又伸长了△L(未超过弹簧的弹性限度),然后使托盘由静止释放,则刚释放托盘时,砝码对托盘的作用力等于( )
如图所示,一根质量不计的轻弹簧上端固定在天花板上,下端与一质量为m的托盘连接,托盘中有一个质量为M的砝码.当托盘静止时,弹簧的伸长量为L.现将托盘向下拉,弹簧又伸长了△L(未超过弹簧的弹性限度),然后使托盘由静止释放,则刚释放托盘时,砝码对托盘的作用力等于( )A、(1+
| ||
B、(1+
| ||
C、
| ||
D、
|
 如图所示,一根质量不计的轻弹簧上端固定在天花板上,下端与一质量为m的托盘连接,托盘中有一个质量为M的砝码.当托盘静止时,弹簧的伸长量为L.现将托盘向下拉,弹簧又伸长了△L(未超过弹簧的弹性限度),然后使托盘由静止释放,则刚释放托盘时,砝码对托盘的作用力等于( )
如图所示,一根质量不计的轻弹簧上端固定在天花板上,下端与一质量为m的托盘连接,托盘中有一个质量为M的砝码.当托盘静止时,弹簧的伸长量为L.现将托盘向下拉,弹簧又伸长了△L(未超过弹簧的弹性限度),然后使托盘由静止释放,则刚释放托盘时,砝码对托盘的作用力等于( )