题目内容
有一质量为m的航天器靠近地球表面绕地球作圆周运动(轨道半径等于地球半径),某时刻航天器启动发动机,在很短的时间内动能变为原来的 ,此后轨道为椭圆,远地点与近地点距地心的距离之比是2:1,经过远地点和经过近地点的速度之比为1:2.己知地球半径为R,地球质量为M,万有引力恒量为G.
,此后轨道为椭圆,远地点与近地点距地心的距离之比是2:1,经过远地点和经过近地点的速度之比为1:2.己知地球半径为R,地球质量为M,万有引力恒量为G.(1)求航天器靠近地球表面绕地球作圆周运动时的动能;
(2)在从近地点运动到远地点的过程中克服地球引力所做的功为多少?
【答案】分析:(1)航天器靠近地球表面绕地球做匀速圆周运动时重力提供向心力,求出速度,根据动能的公式即可求解动能;
(2)先求出喷气后航天器在近地点的动能,根据经过远地点和经过近地点的速度之比为1:2,求出航天器在远日点的动能,由动能定理即可求得克服地球引力做的功.
解答:解:
(1)航天器靠近地球表面绕地球运动时,万有引力提供向心力
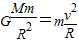 …①
…①
由①得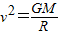
故此时航天器动能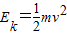 =
=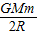
(2)根据题意知,航天器在近地点的动能
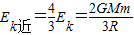
又因为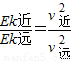 =
=
所以远地点的动能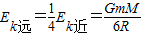
航天器从近地点向远地点运动的过程中只有地球引力做功,根据动能定理有:
W引=Ek远-Ek远=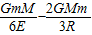 =-
=-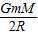
所以克服地球引力所做的功为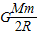
答:(1)航天器靠近地球表面绕地球作圆周运动时的动能为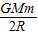 ;
;
(2)在从近地点运动到远地点的过程中克服地球引力所做的功为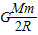 .
.
点评:本题主要考查万有引力提供向心力公式及动能定理的直接应用,难度适中.
(2)先求出喷气后航天器在近地点的动能,根据经过远地点和经过近地点的速度之比为1:2,求出航天器在远日点的动能,由动能定理即可求得克服地球引力做的功.
解答:解:
(1)航天器靠近地球表面绕地球运动时,万有引力提供向心力
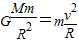 …①
…①由①得
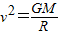
故此时航天器动能
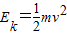 =
=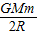
(2)根据题意知,航天器在近地点的动能
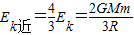
又因为
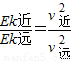 =
=
所以远地点的动能
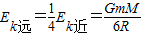
航天器从近地点向远地点运动的过程中只有地球引力做功,根据动能定理有:
W引=Ek远-Ek远=
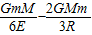 =-
=-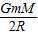
所以克服地球引力所做的功为
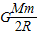
答:(1)航天器靠近地球表面绕地球作圆周运动时的动能为
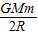 ;
;(2)在从近地点运动到远地点的过程中克服地球引力所做的功为
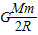 .
.点评:本题主要考查万有引力提供向心力公式及动能定理的直接应用,难度适中.

练习册系列答案
相关题目
 ,此后轨道为椭圆,远地点与近地点距地心的距离之比是2:1,经过远地点和经过近地点的速度之比为 1:2.己知地球半径为R,地球质量为M,万有引力恒量为G.
,此后轨道为椭圆,远地点与近地点距地心的距离之比是2:1,经过远地点和经过近地点的速度之比为 1:2.己知地球半径为R,地球质量为M,万有引力恒量为G.