题目内容
如图所示,质量相等的两个滑块位于光滑水平桌面上,其中弹簧两端分别与静止的滑块N和挡板P相连接,弹簧与挡板的质量均不计;滑块M以初速度v向右运动,它与挡板P碰撞后粘连在一起,在以后的运动过程中( )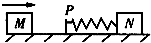
A.M的速度等于0时,弹簧的长度最短
B.M的速度为v/2时,弹簧的弹性势能最大
C.两滑块速度相同时,N的动量最大
D.弹簧的弹力对N做功最多为mv2/2
【答案】分析:两滑块碰撞的过程中动量守恒,M与P碰撞压缩弹簧时,M做减速运动,N做加速运动,开始时M的速度大于N的速度,当M与N速度相等时,弹簧被压缩到最短,此时弹簧弹性势能最大,根据机械能守恒定律可知此时滑块动能之和最小.
解答:解:A、M与P碰撞压缩弹簧时,M做减速运动,N做加速运动,开始时M的速度大于N的速度,当M与N速度相等时,弹簧被压缩到最短,弹簧弹性势能最大,
设相等时的速度为v,根据动量守恒定律得:
mv=2mv
解得v= v0 .故A正确,B错误
v0 .故A正确,B错误
C、弹簧被压缩到最短时,N受弹簧的弹力方向向右,所以继续加速,所以N的动量继续增大,故C错误
D、弹簧被压缩到最短时,弹簧的弹力使得M减速,N加速,当弹簧恢复原长时,
由于两个滑块质量相等,根据动量守恒定律和机械能守恒得M的速度为零,N的速度是v.
根据动能定理得弹簧的弹力对N做功最多为 mv2.故D正确
mv2.故D正确
故选BD.
点评:本题是系统动量守恒和机械能守恒的问题.两个质量相等的小球发生弹性碰撞时,将交换速度.
解答:解:A、M与P碰撞压缩弹簧时,M做减速运动,N做加速运动,开始时M的速度大于N的速度,当M与N速度相等时,弹簧被压缩到最短,弹簧弹性势能最大,
设相等时的速度为v,根据动量守恒定律得:
mv=2mv
解得v=
 v0 .故A正确,B错误
v0 .故A正确,B错误C、弹簧被压缩到最短时,N受弹簧的弹力方向向右,所以继续加速,所以N的动量继续增大,故C错误
D、弹簧被压缩到最短时,弹簧的弹力使得M减速,N加速,当弹簧恢复原长时,
由于两个滑块质量相等,根据动量守恒定律和机械能守恒得M的速度为零,N的速度是v.
根据动能定理得弹簧的弹力对N做功最多为
 mv2.故D正确
mv2.故D正确故选BD.
点评:本题是系统动量守恒和机械能守恒的问题.两个质量相等的小球发生弹性碰撞时,将交换速度.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 如图所示,质量相等的物体A和物体B与地面间的动摩擦因数相等,在力F的作用下,一起沿水平地面向右移动x,则( )
如图所示,质量相等的物体A和物体B与地面间的动摩擦因数相等,在力F的作用下,一起沿水平地面向右移动x,则( )| A、摩擦力对A、B做功不相等 | B、A、B动能的增量相同 | C、F对A做的功与F对B做的功相等 | D、合外力对A做的功与合外力对B做的功相等 |
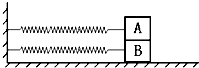 如图所示,质量相等的物块A、B叠放在光滑水平面上.两轻质弹簧的一端固定在竖直墙壁上,另一端分别与A、B相连接.两弹簧的原长相同,与A相连的弹簧的劲度系数小于与B相连的弹簧的劲度系数.开始时A、B处于静止状态.现对物块B施加一水平向右的拉力,使A、B一起向右移动到某一位置又处于静止状态(A、B无相对滑动,弹簧处于弹性限度内),撤去这个拉力后( )
如图所示,质量相等的物块A、B叠放在光滑水平面上.两轻质弹簧的一端固定在竖直墙壁上,另一端分别与A、B相连接.两弹簧的原长相同,与A相连的弹簧的劲度系数小于与B相连的弹簧的劲度系数.开始时A、B处于静止状态.现对物块B施加一水平向右的拉力,使A、B一起向右移动到某一位置又处于静止状态(A、B无相对滑动,弹簧处于弹性限度内),撤去这个拉力后( )| A、A受到的合力总等于弹簧对B的弹力 | B、A受到的合力总大于弹簧对B的弹力 | C、A受到的摩擦力始终与弹簧对它的弹力方向相同 | D、A受到的摩擦力与弹簧对它的弹力方向有时相同,有时相反 |
 如图所示,质量相等的五个物块在光滑水平面上,间隔一定距离排成一条直线.具有初动能E0的物块1向其它4个静止的物块运动,依次发生碰撞,每次碰撞后不再分开.最后5个物块粘成一个整体.这个整体的动能等于( )
如图所示,质量相等的五个物块在光滑水平面上,间隔一定距离排成一条直线.具有初动能E0的物块1向其它4个静止的物块运动,依次发生碰撞,每次碰撞后不再分开.最后5个物块粘成一个整体.这个整体的动能等于( ) (2011?罗湖区模拟)如图所示,质量相等的甲、乙两物体位于同一水平线上的A、B两点.甲作平抛运动,同时乙作自由落体运动.AC为甲的运动轨迹,BC为乙的运动轨迹,两轨迹相交于C点,(空气阻力忽略,两物体距离地面足够高)则两物体( )
(2011?罗湖区模拟)如图所示,质量相等的甲、乙两物体位于同一水平线上的A、B两点.甲作平抛运动,同时乙作自由落体运动.AC为甲的运动轨迹,BC为乙的运动轨迹,两轨迹相交于C点,(空气阻力忽略,两物体距离地面足够高)则两物体( )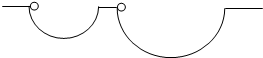 半径为r和R(r<R)的光滑半圆形槽,其圆心均在同一水平面上,如图所示,质量相等的两物体分别自半圆形槽左边缘的最高点无初速地释放,在下滑过程中两物体( )
半径为r和R(r<R)的光滑半圆形槽,其圆心均在同一水平面上,如图所示,质量相等的两物体分别自半圆形槽左边缘的最高点无初速地释放,在下滑过程中两物体( )