题目内容
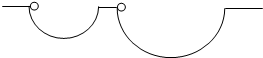 半径为r和R(r<R)的光滑半圆形槽,其圆心均在同一水平面上,如图所示,质量相等的两物体分别自半圆形槽左边缘的最高点无初速地释放,在下滑过程中两物体( )
半径为r和R(r<R)的光滑半圆形槽,其圆心均在同一水平面上,如图所示,质量相等的两物体分别自半圆形槽左边缘的最高点无初速地释放,在下滑过程中两物体( )分析:根据机械能守恒的条件可以判断两小球在光滑圆形槽中下滑过程中机械能是守恒的.由机械能守恒定律,求出小球经过最低点时速度大小,就能比较动能的大小关系.利用向心力知识求出在最低点时,轨道对小球的支持力,进而比较小球对轨道的压力.取圆心所在水平面为参考平面,两小球在水平面上时,机械能均为零,下滑过程中机械能都不变,故确定在最低点时它们的机械能是相等的.
解答:解:A、圆形槽光滑,两小球下滑过程中,均只有重力做功,机械能均守恒.故A错误.
B、根据机械能守恒定律,得
mgr=
mv12 EK1=mgr 同理 EK2=mgR
由于R>r,则 EK1<EK2 故B错误
C、设在最低点时轨道对小球的支持力为FN,则根据牛顿第二定律,得
FN-mg=m
,v=
得到 FN=3mg FN与圆形槽的半径无关.
则在最低点时两球对轨道的压力相等.故C正确.
D、取圆形槽圆心所在水平面为参考平面,
则在最高点时,两球机械能均为零,相等,下滑过程中机械能均守恒,则在最低点时机械能仍相等.故D正确.
故选CD
B、根据机械能守恒定律,得
mgr=
| 1 |
| 2 |
由于R>r,则 EK1<EK2 故B错误
C、设在最低点时轨道对小球的支持力为FN,则根据牛顿第二定律,得
FN-mg=m
| v2 |
| r |
| 2gr |
则在最低点时两球对轨道的压力相等.故C正确.
D、取圆形槽圆心所在水平面为参考平面,
则在最高点时,两球机械能均为零,相等,下滑过程中机械能均守恒,则在最低点时机械能仍相等.故D正确.
故选CD
点评:本题C项是机械能守恒定律和向心力知识的综合,其结论与半径均无关,类似模型如绳子一端固定在悬点,另一端固定一小球,绳子拉直,让小球从和悬点等高的水平面初速释放,小球经过最低点时,绳子的拉力为3mg,高考曾考过.

练习册系列答案
相关题目
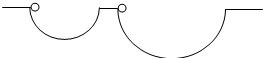 半径为r和R(r<R)的光滑半圆形槽,其圆心均在同一水平面上,如图所示,质量相等的两物体分别自半圆形槽左边缘的最高点无初速地释放,在下滑过程中两物体( )
半径为r和R(r<R)的光滑半圆形槽,其圆心均在同一水平面上,如图所示,质量相等的两物体分别自半圆形槽左边缘的最高点无初速地释放,在下滑过程中两物体( )| A、机械能均逐渐减小 | B、经最低点时动能相等 | C、两球在最低点加速度大小相等 | D、机械能总是相等的 |
 (2012?湖北模拟)半径为r和R(r<R)的光滑半圆形槽,其圆心均在同一水平面上,如图所示,质量相等的两物体分别自半圆形槽左边缘的最高点无初速地释放,在下滑过程中两物体( )
(2012?湖北模拟)半径为r和R(r<R)的光滑半圆形槽,其圆心均在同一水平面上,如图所示,质量相等的两物体分别自半圆形槽左边缘的最高点无初速地释放,在下滑过程中两物体( )
