Question

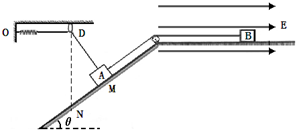（2013?四川）在如图所示的竖直平面内，物体A和带正电的物体B用跨过定滑轮的绝缘轻绳连接，分别静止于倾角θ=37⁰的光滑斜面上的M点和粗糙绝缘水平面上，轻绳与对应平面平行．劲度系数K=5N/m的轻弹簧一端固定在0点，一端用另一轻绳穿过固定的光滑小环D与A相连，弹簧处于原长，轻绳恰好拉直，DM垂直于斜面．水平面处于场强E=5×10⁴N/C、方向水平向右的匀强电场中．已知A、B的质量分别为m_A=0.1kg和m_B=0.2kg，B所带电荷量q=+4×l0^-6C．设两物体均视为质点，不计滑轮质量和摩擦，绳不可伸长，弹簧始终在弹性限度内，B电量不变．取g=lOm/s²，sin37°=0.6，cos37°=0.8．
（1）求B所受静摩擦力的大小；
（2）现对A施加沿斜面向下的拉力F，使A以加速度a=0.6m/s²开始做匀加速直线运动．A从M到N的过程中，B的电势能增加了△E_p=0.06J．已知DN沿竖直方向，B与水平面间的动摩擦因数μ=0.4．求A到达N点时拉力F的瞬时功率．

Answer 1

分析：（1）分别对A和B受力分析，根据共点力平衡求出B所受摩擦力的大小．
（2）通过电势能的变化，得出电场力做功，从而得出B移动的距离，根据几何关系求出弹簧的形变量，通过对A在N点、以及B受力分析，根据牛顿第二定律结合胡克定律，求出拉力F的大小，

解答：解：（1）据题意 静止时 受力分析如图所示
由 平衡条件 得：
对A有   m_Agsinθ=F_T     ①
对B有   qE+f₀=F_T      ②
代入数据得f₀=0.4 N         ③
（2）据题意 A到N点时 受力分析 如图所示由 牛顿第二定律 得：
对A有   F+m_Agsinθ-F_T-F_Ksinθ=m_Aa   ④
对B有   F_T-qE-f=m_Ba                 ⑤
其中  f=μm_Bg            ⑥
F_K=kx                     ⑦
由电场力做功与电势能的关系得△E_P=qEd          ⑧
由几何关系得x=

d

sinθ

-

d

tanθ

              ⑨
A由M到N  由 

v

2 t

-

v

2 0

=2ad 得 A运动到N的速度v=

2ad

                           ⑩
拉力F在N点的瞬时功率       P=Fv?
由以上各式 代入数据 P=0.528 W?
答：（1）B所受静摩擦力的大小为0.4N．
（2）A到达N点时拉力F的瞬时功率为0.528W．

点评：本题综合考查了共点力平衡、牛顿第二定律、胡克定律、电场力做功与电势能的关系，以及运动学公式，综合性较强，对学生的能力要求较高，需加强训练．