题目内容
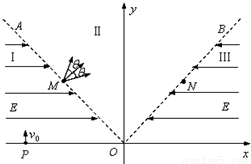
如图所示为某一仪器的部分原理示意图,虚线OA、OB关于y轴对称,且∠AOB=90°,OA、OB将xOy平面分为Ⅰ、Ⅱ、Ⅲ三个区域,区域Ⅰ、Ⅲ内存在水平方向的匀强电场,电场强度大小均为E、方向相反.现有质量为m,电量为+q(q>0)的大量带电粒子从x轴上的粒子源P处以速度v沿y轴正方向射出,到达OA上的M点时速度与OA垂直.(不计粒子的重力及粒子间的相互作用)求:(1)粒子从P点运动到M点的时间;
(2)为使粒子能从M点经Ⅱ区域通过OB上的N点,M、N点关于y轴对称,可在区域Ⅱ内加一垂直xOy平面的匀强磁场,求该磁场的磁感应强度的最小值和粒子经过区域Ⅲ到达x轴上Q点的横坐标;
(3)当匀强磁场的磁感应强度取(2)问中的最小值时,且该磁场仅分布在区域Ⅱ内的一个圆形区域内.由于某种原因的影响,粒子经过M点时的速度并不严格与OA垂直,成散射状,散射角为θ,但速度大小均相同,如图所示.求所有粒子经过OB时的区域长度.
【答案】分析:(1)粒子在Ⅰ区域做类平抛运动,有运动位移可得时间
(2)使粒子通过N点且磁感应强度最小,则粒子在Ⅱ内做匀速圆周运动半径R=OM,粒子经N点后进入Ⅲ区域,做匀变速曲线运运动,有运动分解知识求得到达x轴上Q点的横坐标
(3)该圆形磁场区域的半径r等于其轨迹圆半径R,分别作出两边缘状态的轨迹图,由几何关系求解
解答: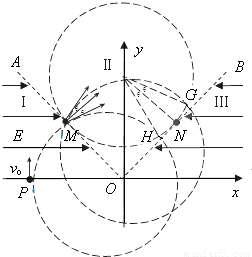 解:(1)粒子在Ⅰ区内做类平抛运动,设运动的时间为t
解:(1)粒子在Ⅰ区内做类平抛运动,设运动的时间为t
则: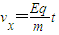 ①
①
vx=v②
由 ①②两式得: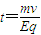 ③
③
(2)粒子在Ⅰ区内y方向的位移:y=vt
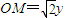
使粒子通过N点且磁感应强度最小,则粒子在Ⅱ内做匀速圆周运动半径R=OM④
由③④⑤式,可得: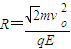 ⑤
⑤
又由洛仑兹力和牛顿第二定律可得,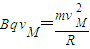 ⑥
⑥
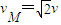 ⑦
⑦
由上式可得: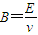 ⑧
⑧
粒子进入Ⅲ区后,运动的轨迹PM与QN对称,故:OQ=OP⑨
又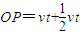 =10 ⑩
=10 ⑩
得: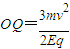
故:Q点的坐标为(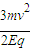 ,0)
,0)
(3)该圆形磁场区域的半径r等于其轨迹圆半径R,即:
r=R=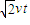
所有粒子出磁场时速度方向平行,其落点在直线OB上的GH两点之间,如图:
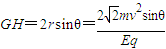
答:(1)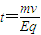 ;(2)Q点的坐标为(
;(2)Q点的坐标为(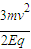 ,0);(3)
,0);(3)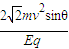
点评:本题考查带电粒子在电场和磁场中的运动,关键理清粒子的运动轨迹,以及运动的情况,结合几何关系进行求解.
(2)使粒子通过N点且磁感应强度最小,则粒子在Ⅱ内做匀速圆周运动半径R=OM,粒子经N点后进入Ⅲ区域,做匀变速曲线运运动,有运动分解知识求得到达x轴上Q点的横坐标
(3)该圆形磁场区域的半径r等于其轨迹圆半径R,分别作出两边缘状态的轨迹图,由几何关系求解
解答:
 解:(1)粒子在Ⅰ区内做类平抛运动,设运动的时间为t
解:(1)粒子在Ⅰ区内做类平抛运动,设运动的时间为t则:
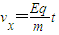 ①
①vx=v②
由 ①②两式得:
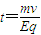 ③
③(2)粒子在Ⅰ区内y方向的位移:y=vt
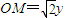
使粒子通过N点且磁感应强度最小,则粒子在Ⅱ内做匀速圆周运动半径R=OM④
由③④⑤式,可得:
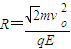 ⑤
⑤又由洛仑兹力和牛顿第二定律可得,
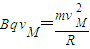 ⑥
⑥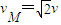 ⑦
⑦由上式可得:
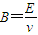 ⑧
⑧粒子进入Ⅲ区后,运动的轨迹PM与QN对称,故:OQ=OP⑨
又
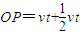 =10 ⑩
=10 ⑩得:
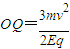
故:Q点的坐标为(
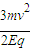 ,0)
,0)(3)该圆形磁场区域的半径r等于其轨迹圆半径R,即:
r=R=
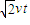
所有粒子出磁场时速度方向平行,其落点在直线OB上的GH两点之间,如图:
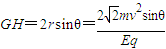
答:(1)
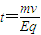 ;(2)Q点的坐标为(
;(2)Q点的坐标为(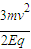 ,0);(3)
,0);(3)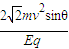
点评:本题考查带电粒子在电场和磁场中的运动,关键理清粒子的运动轨迹,以及运动的情况,结合几何关系进行求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2012?邯郸模拟)如图所示为某一仪器的部分原理示意图,虚线OA、OB关于y轴对称,且∠AOB=90°,OA、OB将xOy平面分为Ⅰ、Ⅱ、Ⅲ三个区域,区域Ⅰ、Ⅲ内存在水平方向的匀强电场,电场强度大小均为E、方向相反.现有质量为m,电量为+q(q>0)的大量带电粒子从x轴上的粒子源P处以速度v0沿y轴正方向射出,到达OA上的M点时速度与OA垂直.(不计粒子的重力及粒子间的相互作用)求:
(2012?邯郸模拟)如图所示为某一仪器的部分原理示意图,虚线OA、OB关于y轴对称,且∠AOB=90°,OA、OB将xOy平面分为Ⅰ、Ⅱ、Ⅲ三个区域,区域Ⅰ、Ⅲ内存在水平方向的匀强电场,电场强度大小均为E、方向相反.现有质量为m,电量为+q(q>0)的大量带电粒子从x轴上的粒子源P处以速度v0沿y轴正方向射出,到达OA上的M点时速度与OA垂直.(不计粒子的重力及粒子间的相互作用)求: 如图所示为某一仪器的部分原理示意图,虚线OA、OB关于y轴对称,∠AOB=90°,OA、OB将xOy平面分为Ⅰ、Ⅱ、Ⅲ三个区域,区域Ⅰ、Ⅲ内存在水平方向的匀强电场,电场强度大小相等、方向相反.带电粒子自x轴上的粒子源P处以速度v0沿y轴正方向射出,经时间t到达OA上的M点,且此时速度与OA垂直.已知M到原点O的距离OM=a,不计粒子的重力.求:
如图所示为某一仪器的部分原理示意图,虚线OA、OB关于y轴对称,∠AOB=90°,OA、OB将xOy平面分为Ⅰ、Ⅱ、Ⅲ三个区域,区域Ⅰ、Ⅲ内存在水平方向的匀强电场,电场强度大小相等、方向相反.带电粒子自x轴上的粒子源P处以速度v0沿y轴正方向射出,经时间t到达OA上的M点,且此时速度与OA垂直.已知M到原点O的距离OM=a,不计粒子的重力.求:

 , OA、OB将xOy平面分为Ⅰ、Ⅱ、Ⅲ三个区域,区域Ⅰ、Ⅲ内存在水平方向的匀强电场,电场强度大小相等、方向相反。质量为m电荷量为q的带电粒子自x轴上的粒子源P处以速度v0沿y轴正方向射出,经一定时间到达OA上的M点,且此时速度与OA垂直。已知M到原点O的距离OM = L,不计粒子的重力。求:
, OA、OB将xOy平面分为Ⅰ、Ⅱ、Ⅲ三个区域,区域Ⅰ、Ⅲ内存在水平方向的匀强电场,电场强度大小相等、方向相反。质量为m电荷量为q的带电粒子自x轴上的粒子源P处以速度v0沿y轴正方向射出,经一定时间到达OA上的M点,且此时速度与OA垂直。已知M到原点O的距离OM = L,不计粒子的重力。求:
 (
(